网络流Edmonds-Karp算法入门

今天自习课没事干，看书自学了一下网络流中的EK算法。(求最大流)

设s为源点，t为汇点，C为容量矩阵，F为流量矩阵，f为最大流量。

1.初始化F,f

2.用BFS在残量网络中找到一条从s到t的最短增广路T，如果T不存在，算法结束。

　　最短增广路就是最短路径(s→t)

　　一边(u,v)被增广完后，在残量网络中就不存在(u,v)这条边，只有(v,u)这条边了。(即不存在(u,v)这条路径)

3.m=min_(u,v)∈T{C(u,v)-F(u,v)} (最短增广路径中残量网络中最小的边)

4.f+=m

5.沿着T修改矩阵，对于任意(u,v)∈T，将F(u,v)增加m，F(u,v)减少m

　　F(u,v)之所以要减少m是因为有可能会出现以下情况：

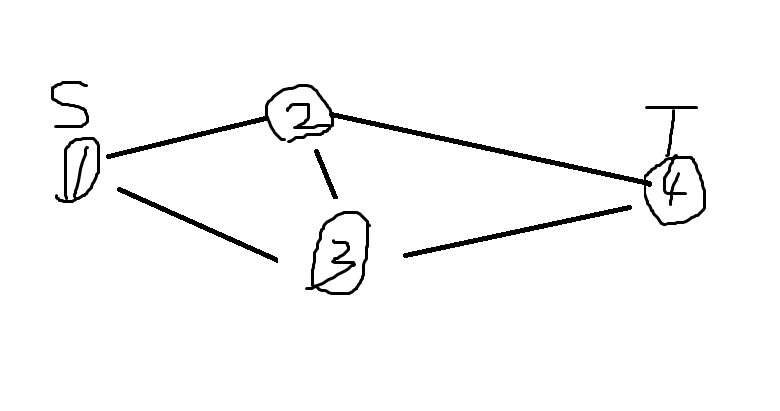
　　假设求出增广路径1→2→3→4

　　但发现其实1→3→4+1→2→4更优

　　这就需要反向建边

6.repeat 2.

code:

#include <cstdio>
#include <cstring>
#include <algorithm>
#define F(i,x,y) for(int i=x;i<=y;i++)
using namespace std;

const int MAXN=;
int N,M,a[MAXN][MAXN];
int pre[MAXN],vis[MAXN],l[MAXN],h,t,S,T;

int BFS()
{
    memset(pre,-,sizeof(pre));
    memset(vis,,sizeof(vis));
    h=t=;pre[S]=S,vis[S]=;l[++t]=S;
        while(h<t){
            int P=l[++h];
            for(int i=;i<=N;i++){
                if(a[P][i]>&&!vis[i]){
                    vis[i]=;
                    pre[i]=P;
                    if(i==T)return true;
                    l[++t]=i;
                }
            }
        }
    return false;
}

int EK()
{
    int F=,w=2e9;
        while(BFS()){
            for(int i=T;i!=S;i=pre[i])w=min(w,a[pre[i]][i]);
            for(int i=T;i!=S;i=pre[i]){
                a[i][pre[i]]+=w;
                a[pre[i]][i]-=w;
            }
            F+=w;
        }
    return F;
}

int main()
{
    while(scanf("%d%d%d%d",&N,&M,&S,&T)!=EOF){
        memset(a,,sizeof(a));
        int u,v,w;
            F(i,,M){
                scanf("%d%d%d",&u,&v,&w);
                a[u][v]+=w;
            }
        printf("%d\n",EK());
    }return ;
}