numpy.linalg.norm(求范数)

1、linalg=linear（线性）+algebra（代数），norm则表示范数。

2、函数参数

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)  　

　　①x: 表示矩阵（也可以是一维）

　　②ord：范数类型

　　向量的范数：

　　

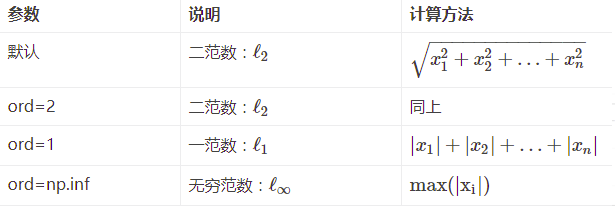
　　矩阵的范数：

　　　　ord=1：列和的最大值

　　　　ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根

　　　　ord=∞：行和的最大值

　　③axis：处理类型

　　　　axis=1表示按行向量处理，求多个行向量的范数

　　　　axis=0表示按列向量处理，求多个列向量的范数

　　　　axis=None表示矩阵范数。

　　④keepding：是否保持矩阵的二维特性

　　　　True表示保持矩阵的二维特性，False相反

3、代码实现

import numpy as np
x = np.array([
    [0, 3, 4],
    [1, 6, 4]])
#默认参数ord=None，axis=None，keepdims=False
print "默认参数(矩阵2范数，不保留矩阵二维特性)：",np.linalg.norm(x)
print "矩阵2范数，保留矩阵二维特性：",np.linalg.norm(x,keepdims=True)  

print "矩阵每个行向量求向量的2范数：",np.linalg.norm(x,axis=1,keepdims=True)
print "矩阵每个列向量求向量的2范数：",np.linalg.norm(x,axis=0,keepdims=True)  

print "矩阵1范数：",np.linalg.norm(x,ord=1,keepdims=True)
print "矩阵2范数：",np.linalg.norm(x,ord=2,keepdims=True)
print "矩阵∞范数：",np.linalg.norm(x,ord=np.inf,keepdims=True)  

print "矩阵每个行向量求向量的1范数：",np.linalg.norm(x,ord=1,axis=1,keepdims=True)  

结果显示：

　　

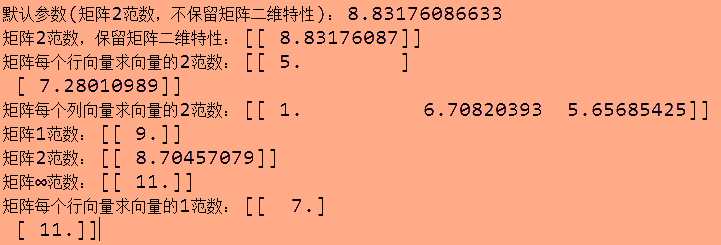
4、总结

①矩阵的三种范数求法

②向量的三种范数求法