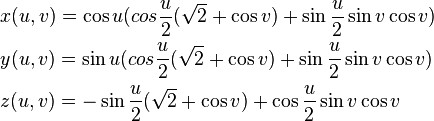数学图形之克莱因瓶(klein bottle)
克莱因瓶是一种内外两面在同一个曲面上的图形.
在数学领域中,克莱因瓶(德语:Kleinsche Flasche)是指一种无定向性的平面,比如二维平面,就没有“内部”和“外部”之分。克莱因瓶最初的概念提出是由德国数学家菲利克斯·克莱因提出的。克莱因瓶和我上一篇讲的莫比乌斯带非常相像。一个是内外两面是在同一个曲面上,另一个是里外两面在同一个曲面上.
克莱因瓶的形状是,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。
下面将展示几种莫比乌斯带的生成算法和切图,使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.
以下是从维基上查到的公式
克莱因瓶的参数十分复杂:
写成我的脚本代码为:
vertices = D1: D2:
u = from to PI D1
v = from to (*PI) D2
a = sin(u)
b = cos(u)
c = sin(v)
d = cos(v)
e = *d - *b*b*d - *pow(b, )*d + *pow(b, )*d - *a + *b*d*a - *pow(b, )*d*a - *pow(b, )*d*a + *pow(b, )*d*a
x = -/*b*(*d - *a + *pow(b, )*a - *pow(b, )*a + *b*d*a)
y = -/*a*e
z = /*( + *b*a)*c u = u*
v = v*2.5
公式好复杂,我竟然写对了:

还有一个较简单的
写成我的脚本代码为:
vertices = D1: D2:
u = from to (*PI) D1
v = from to (*PI) D2 a = sin(u)
b = cos(u) c = sin(v)
d = cos(v) e = sin(u/)
f = cos(u/) x = b*(f*(sqrt() + d) + e*c*d)
z = a*(f*(sqrt() + d) + e*c*d)
y = -e*(sqrt() + d) + f*c*d
可惜这似乎是错的.生成的图形不是克莱因瓶.

此外,我还从别的地方找到关于克莱因瓶的公式.这两个公式生成的图形差不多,也不像克莱因瓶,而是一个8字形的曲线绕圈而成的曲面.
klein_bottle
#http://xahlee.info/surface/klein_bottle/klein_bottle.html vertices = D1: D2: u = from to (PI*) D1
v = from to (PI*) D2 a = x = (a+cos[v/]*sin[u]-sin[v/]*sin[*u])*cos[v]
z = (a+cos[v/]*sin[u]-sin[v/]*sin[*u])*sin[v]
y = sin[v/]*sin[u]+cos[v/]*sin[*u]

klein
#http://www.mathcurve.com/surfaces/klein/klein.shtml
vertices = D1: D2:
u = from to (PI*) D1
v = from to (PI*) D2
a = rand2(, )
b = rand2(, )
x = [a + b*(cos(u/)*sin(v) - sin(u/)*sin(*v))]*cos(u)
z = [a + b*(cos(u/)*sin(v) - sin(u/)*sin(*v))]*sin(u)
y = b*[sin(u/)*sin(v) + cos(u/)*sin(*v)]

数学图形之克莱因瓶(klein bottle)的更多相关文章
- WHY数学图形可视化工具(开源)
WHY数学图形可视化工具 软件下载地址:http://files.cnblogs.com/WhyEngine/WhyMathGraph.zip 源码下载地址: http://pan.baidu.com ...
- 数学图形(1.49)Nephroid曲线
昨天IPhone6在国内发售了,我就顺手发布个关于肾的图形.Nephroid中文意思是肾形的.但是这种曲线它看上去却不像个肾,当你看到它时,你觉得它像什么就是什么吧. The name nephroi ...
- 数学图形(1.48)Cranioid curve头颅线
这是一种形似乎头颅的曲线.这种曲线让我想起读研的时候,搞的医学图像三维可视化.那时的原始数据为脑部CT图像.而三维重建中有一种方式是面绘制,是将每一幅CT的颅骨轮廓提取出来,然后一层层地罗列在一起,生 ...
- 数学图形之贝塞尔(Bézier)曲面
前面章节中讲了贝塞尔(Bézier)曲线,而贝塞尔曲面是对其多一个维度的扩展.其公式依然是曲线的公式: . 而之所以由曲线变成曲面,是将顶点横向连了再纵向连. 很多计算机图形学的教程都会有贝塞尔曲面的 ...
- 数学图形(1.47)贝塞尔(Bézier)曲线
贝塞尔曲线又称贝兹曲线或贝济埃曲线,是由法国数学家Pierre Bézier所发现,由此为计算机矢量图形学奠定了基础.它的主要意义在于无论是直线或曲线都能在数学上予以描述. 上一节讲的是高次方程曲线, ...
- 数学图形之Breather surface
这是一种挺漂亮的曲面图形,可惜没有找到太多的相关解释. In differential equations, a breather surface is a mathematical surface ...
- 数学图形之Kuen Surface
Kuen Surface应该又是一个以数学家名字命名的曲面.本文将展示几种Kuen Surface的生成算法和切图,其中有的是标准的,有的只是相似.使用自己定义语法的脚本代码生成数学图形.相关软件参见 ...
- 数学图形之Boy surface
这是一个姓Boy的人发现的,所以取名为Boy surface.该图形与罗马图形有点相似,都是三分的图形.它甚至可以说是由罗马曲面变化而成的. 本文将展示几种Boy曲面的生成算法和切图,使用自己定义语法 ...
- 数学图形之SineSurface与粽子曲面
SineSurface直译为正弦曲面.这有可能和你想象的正弦曲线不一样.如果把正弦曲线绕Y轴旋转,得到的该是正弦波曲面.这个曲面与上一节中的罗马曲面有些相似,那个是被捏过的正四面体,这个则是个被捏过正 ...
随机推荐
- HP电脑的增霸卡功能操作详解
机房管理中HP电脑的增霸卡功能操作详解 一.软件去除保护 1).电脑开机后等待进入增霸卡选择系统界面: 2).按F1帮助,F10进入增霸卡BIOS界面: 3).光标切换到>>>系统还 ...
- 美团客户端响应式框架EasyReact开源啦
前言 EasyReact 是一款基于响应式编程范式的客户端开发框架,开发者可以使用此框架轻松地解决客户端的异步问题. 目前 EasyReact 已在美团和大众点评客户端的部分业务中进行了实践,并且持续 ...
- FGPA 中的计数器Verilog语言(时钟分频器)
在quartusII8.0中为ALTERAFPGA设置一个分频器(计数器) 输入时钟48Mhz 输出时钟9600HZ /* 实验名称: 计数器 ** 程序功能: 将48Mhz的时钟分频为9600Hz ...
- tensorflow模块安装
有时候,我们的电脑上或许会同时安装多个python的环境,譬如,我的电脑上同时装了anaconda2和3. 在安装的时候,譬如,我想在python3中装tensorflow,则需要在 C:\Progr ...
- hdu 4547 LCA **
题意:在Windows下我们可以通过cmd运行DOS的部分功能,其中CD是一条很有意思的命令,通过CD操作,我们可以改变当前目录. 这里我们简化一下问题,假设只有一个根目录,CD操作也只有两种方式: ...
- Python168的学习笔记8
#coding:utf8 #斐波那契数列,第三项起,每一项都等于前两项之和 def memo(func): cache = {}#闭包 def wrap(*args): if args not in ...
- Minimum Size Subarray Sum 最短子数组之和
题意 Given an array of n positive integers and a positive integer s, find the minimal length of a suba ...
- linux—文件目录简单介绍
1.Linux系统以文件目录的方式来组织和管理系统中的所有文件.所谓文件目录就是将所有文件的说明信息采用树型结构组织起来,即我们常说的目录:整个文件系统有一个“根”(root),然后在根上分“杈”(d ...
- mysql反向解析导致连接缓慢
Content 0.序 1.问题 2.原因 3.解决办法 0.序 本文主要是记录Mysql安装在 VMWARE下,本地连接Mysql速度很慢的原因及解决办法. 1.问题 本地的一个网站使用mysql数 ...
- 【Deep Learning】一、AutoEncoder
Deep Learning 第一战: 完成:UFLDL教程 稀疏自编码器-Exercise:Sparse Autoencoder Code: 学习到的稀疏参数W1: 参考资料: UFLDL教程 稀疏自 ...