[UVA 10635] Prince ans Princess

图片加载可能有点慢，请跳过题面先看题解，谢谢

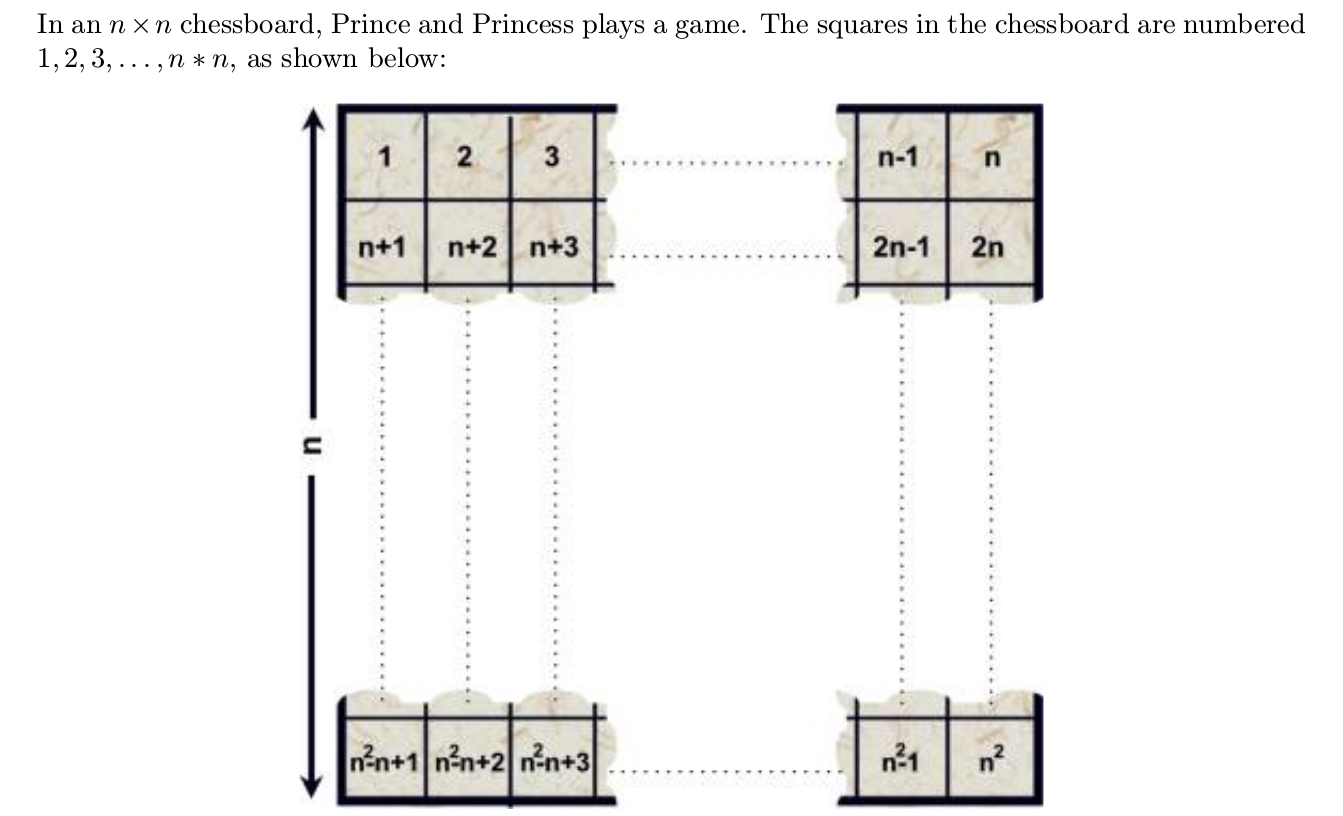
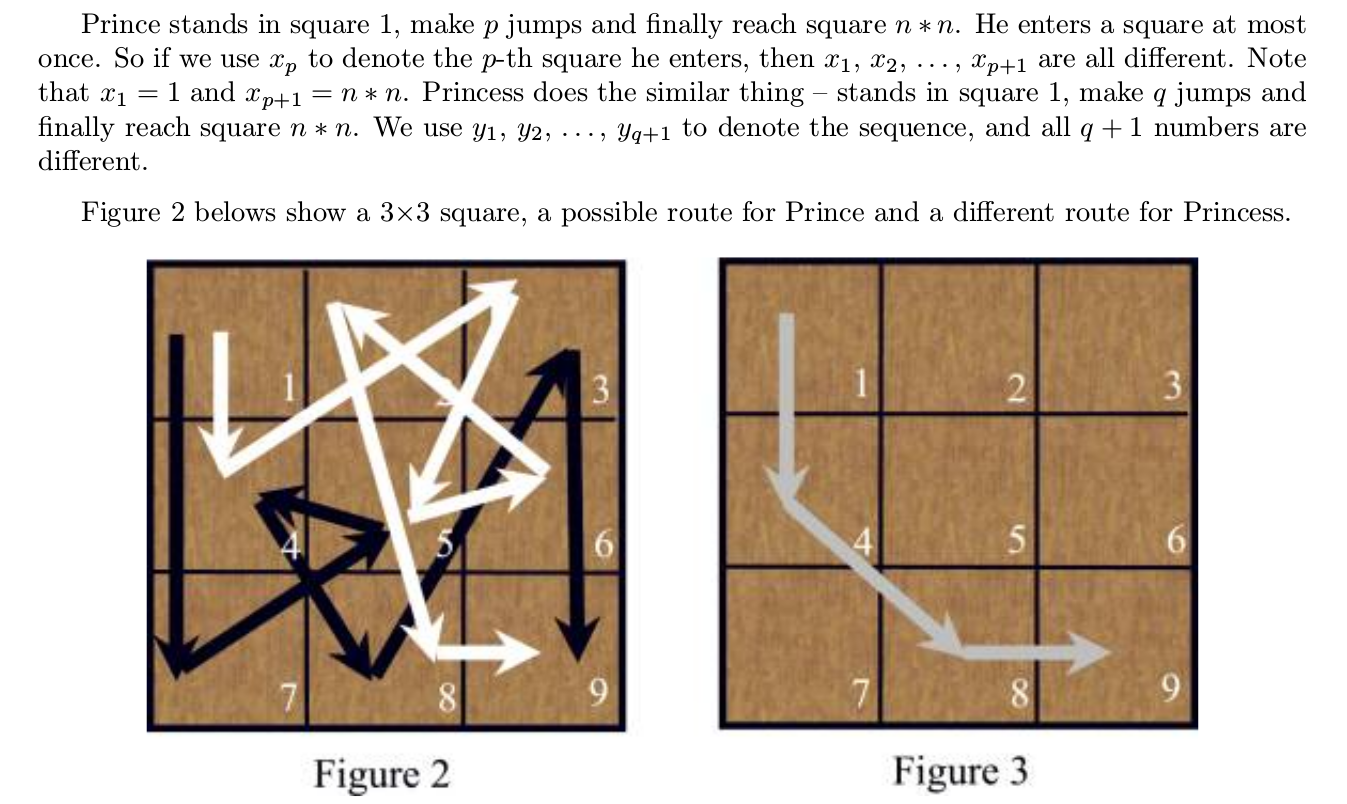
这道题。。。
还是要点思维的。。。
第一眼看是个最长公共子序列，但是， \(N\le 62500\) ，并不能 \(O(n^2)\) 求
$
$
这道题有个很好的性质，每个序列中的元素互不相同
也就是说，在一个序列中，每一个数字都有一个唯一的位置
这有什么用？
$
$
我们进行这样一个操作，把 \(b\) 序列中的数字换成该数字在 \(a\) 序列中出现的位置，那么问题就变成了一个求 \(b\) 序列的 \(LCS\) 的问题了
这样我们就可以在 \(O(nlogn)\) 的复杂度下解决这个问题

再吐槽一下。。。
做这道题目，思考 \(10min\) ，代码调试 \(2h\) ，震惊，原因竟是？
看下这个语句：
我写的： \(a[++k]=max(a[k],x)\)
AC程序： \(a[k+1]=max(a[k+1],x)\)，或者 \(a[k]=max(a[++k],x)\)

//made by Hero_of_Someone
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define il inline
#define RG register
using namespace std;
il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();
  if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }

int T,t,N,n,m,cnt;
int a[100010],b[100010],id[100010];

il void init(){
   N=gi(),n=gi()+1,m=gi()+1;
   memset(id,0,sizeof(id)); cnt=0;
   for(RG int i=1;i<=n;i++) a[i]=gi(),id[a[i]]=i;
   for(RG int i=1;i<=m;i++){ b[i]=gi();
      if(id[b[i]]) b[++cnt]=id[b[i]];
   }
}

il void work(){
   n=cnt,cnt=0;
   memset(a,0x3f3f3f3f,sizeof(a));
   for(RG int i=1;i<=n;i++){
      RG int x=b[i];
      RG int l=1,r=cnt,k=0;
      while(l<=r){
         RG int mid=(l+r)>>1;
         if(a[mid]>x) r=mid-1;
         else l=mid+1,k=mid;
      }
      if(k==cnt) a[++cnt]=x;
      else a[k]=min(a[++k],x);
   }
   printf("Case %d: %d\n",t,cnt);
}

int main(){ T=gi(); for(t=1;t<=T;t++){ init(); work(); } return 0; }