BZOJ2876 [Noi2012]骑行川藏 【拉格朗日乘数法】

题目链接

BZOJ

题解

拉格朗日乘数法

拉格朗日乘数法用以求多元函数在约束下的极值

我们设多元函数\(f(x_1,x_2,x_3,\dots,x_n)\)

以及限制\(g(x_1,x_2,x_3,\dots,x_n) = E\)

我们需要求\(f\)在限制\(g\)下的极值

如图



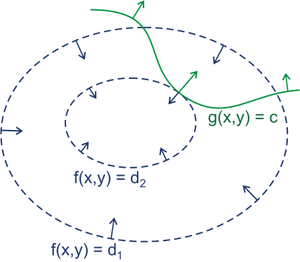
当\(f\)取到最值时，必然与\(g\)的等高线相切

所以我们只需找出这个切点

切点处两函数的梯度向量平行\({\nabla f~//~\nabla g}\)

梯度向量的每一维就是该维下的偏导函数

\[{\nabla f=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3},\dots,\frac{\partial f}{\partial x_n})}
\]

偏导可以理解为把别的变量看做常数，只对一个变量求导

所以只需令

\[\nabla f = \lambda \nabla g
\]

可以得到\(n\)个方程，加上\(g\)本身就是一个方程

可以得到\(n + 1\)个方程，可解\(\lambda\)以及\(x_i\)

本题

限制是

\[\sum\limits_{i = 1}^{n}s_ik_i(v_i - v'_i)^{2} = E
\]

我们要最小化

\[\sum\limits_{i = 1}^{n}\frac{s_i}{v_i}
\]

利用拉格朗日乘数法，我们求出\(n + 1\)个方程

对于变量\(x_i\)的偏导，可得到方程

\[2\lambda k_iv_i^{2}(v_i - v'_i) = -1
\]

首先\(v_i \ge v'_i\)，所以除\(\lambda\)外左边是正的，所以\(\lambda\)是负的，然后可以发现\(v_i\)关于\(\lambda\)单调

而方程

\[\sum\limits_{i = 1}^{n}s_ik_i(v_i - v'_i)^{2} = E
\]

左边也关于\(v_i\)单调，所以可以使用二分求解

当然求\(v_i\)也可以用牛顿迭代

还有就是精度要开够大。。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 10005,maxm = 100005;
const double eps = 1e-13,INF = 1e12;
int n;
double E,v1[maxn],v[maxn],s[maxn],k[maxn];
inline double f(int i,double lam){
	return 2 * lam * k[i] * v[i] * v[i] * (v[i] - v1[i]) + 1;
}
inline double cal(double lam){
	REP(i,n){
		double l = max(v1[i],0.0),r = INF;
		while (r - l > eps){
			v[i] = (l + r) / 2.0;
			if (f(i,lam) >= 0) l = v[i];
			else r = v[i];
		}
		v[i] = l;
	}
	double re = 0;
	REP(i,n) re += s[i] * k[i] * (v[i] - v1[i]) * (v[i] - v1[i]);
	return re;
}
int main(){
	scanf("%d%lf",&n,&E);
	REP(i,n) scanf("%lf%lf%lf",&s[i],&k[i],&v1[i]);
	double l = -INF,r = 0,mid;
	while (r - l > eps){
		mid = (l + r) / 2.0;
		if (cal(mid) >= E) r = mid;
		else l = mid;
	}
	cal(l);
	double ans = 0;
	REP(i,n) ans += s[i] / v[i];
	printf("%.10lf\n",ans);
	return 0;
}