hdu 1817 Necklace of Beads（Polya定理）

Necklace of Beads

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 630    Accepted Submission(s): 232

Problem Description

Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 40 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there?

 

Input

The input has several lines, and each line contains the input data n. 
-1 denotes the end of the input file.

Output

The output should contain the output data: Number of different forms, in each line correspondent to the input data.

 

Sample Input

4

5

-1

 

Sample Output

21

39

 

Source

Xi'an 2002

Recommend

We have carefully selected several similar problems for you:  2481 3547 1812 1465 1398 

 

题解：

这道题和POJ2409是一样的题目，只不过这道题规定了颜色数目。

Polya定理的应用。先来看Polya定理。

Polya定理：设 G = {a1，a2，…，ag}是 N 个对象的置换群，用 M 种颜色给这 N 个对象着色，则不同的着色 方案数为：

|G|^(-1) * {M^c(a1) + M^c(a2) + … + M^c(ag)}。

其中 c(ai)为置换 ai 的循环节数，( i = 1，2，…，g )。

对于这道题，直接用Polya定理求解，找出所有的置换，并求出置换的循环节数。然后根据上边公式求出 3^c(ai) 的总和，再除以置换群个数。

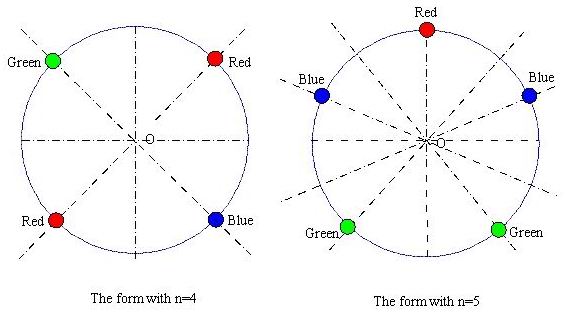
题中有两种置换方式：

1.旋转置换。分别顺时针旋转 i 个珠子，其循环节长度为 LCM(N，i) / i，循环节数为

N / (LCM(N，i) / i)，即 GCD(N，i)。

2.翻转置换。根据 N 的奇偶性分情况讨论。

N为奇数时：

以第 i 个珠子为顶点和中心翻转，翻转后，第 i 个珠子保持不变，其余珠子两两相互对换，因为有 N 个珠子，所以有 N 种翻转置换，每种翻转循环节数为 (N+1) / 2。

N为偶数时，有两种翻转方式：

以两边相对的两个珠子为轴和中心翻转，翻转后，这两个珠子保持不变，其余珠子两两相互对换，共有 N/2 种翻转置换，每种翻转循环节数为 (N+2) / 2。

以相邻的珠子中间连线为轴和中心翻转，翻转后，所有珠子两两相互对换，共有 N/2种翻转置换，每种翻转循环节数为 N/2。

注： 用long long 或__int64定义，本题的n可能是0，所以刚开始错误是RE，要特殊判断。

#include <iostream>
#include<cstdio>
#include<cstring>
#include<cmath>

using namespace std;
long long res,n;
long long gcd(long long a,long long b)
{
    return b?gcd(b,a%b):a;
}
long long poww(long long a,long long b)
{
    long long ans=;
    while(b)
    {
        if (b%==) ans*=a;
        a*=a;
        b/=;
    }
    return ans;
}
int main()
{
    while(~scanf("%lld",&n))
    {
        if (n==-) break;
        if(n<=)
            {printf("0\n"); continue;}

        res=;
        for(long long i=;i<=n;i++)
          res+=poww((long long),gcd(n,i));
        if(n%==)
          res+=poww((long long),(n+)/)*n;
        else
        {
           res+=poww((long long),n/+)*(n/);
           res+=poww((long long),n/)*(n/);
        }
        printf("%lld\n",res/(*n));
    }
    return ;
}

转自：http://blog.csdn.net/lianai911/article/details/48271557