显示等待WebDriverWait+EC

参考：https://www.cnblogs.com/yoyoketang/p/6538505.html

百度搜索关键字，等待搜索结果页面显示完成后，验证搜索结果的第一条记录

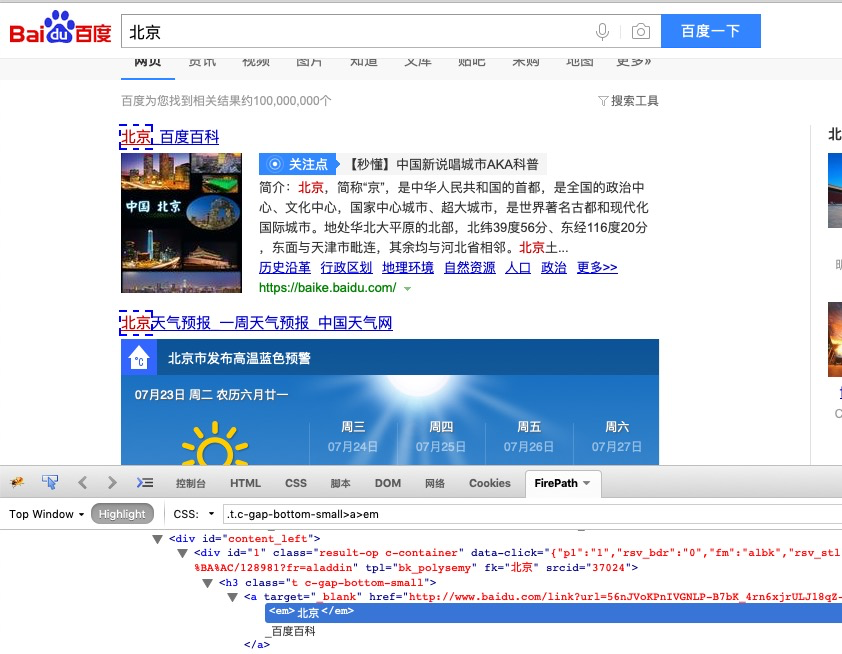
通过WebDriverWait定位一组元素

如果是定位一组元素，用到presence_of_all_elements_located，定位一个元素presence_of_element_located

presence_of_all_elements_located和presence_of_element_located区别：

presence_of_element_located : 判断某个元素是否被加到了dom树里，并不代表

presence_of_all_elements_located : 判断是否至少有1个元素存在于dom树中。举个例子，如果页面上有n个元素的class都是'column-md-3'，那么只要有1个元素存在，这个方法就返回True

代码如下：

#coding:utf-8
'''
这里写了一个百度搜索页的pageobject
'''
from PageElement.readYaml import parseyaml
from selenium.webdriver.support.wait import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC

class Baidu_page():
    '''
    百度搜索page类
    '''

    getElement = parseyaml()

    search_box = getElement["baiduPage"]["search_box"]["value"]
    baidu_button = getElement["baiduPage"]["baidu_button"]["value"]
    search_result = getElement["baiduPage"]["search_result"]["value"]

    def __init__(self,driver):
        self.driver = driver

    def input_search(self,keyword,type_a="css"):
        '''输入搜索关键词'''
        self.driver.find_element(type_a,self.search_box).send_keys(keyword)

    def click_baidubutton(self,type_a="css"):
        '''点击百度一下按钮'''
        self.driver.find_element(type_a, self.baidu_button).click()

    def verification_result(self,type_a="css"):
        '''用例结果验证'''
        results = WebDriverWait(self.driver,10).until(EC.presence_of_all_elements_located((type_a,self.search_result)))
        print(results)

        nanjing_baike = results[0].text
        return nanjing_baike