【CDN+】 Kylin 的初步认识与理解

前言

项目中用到了Kylin框架来处理数据，那么作为项目成员需要了解哪些关于Kylin的知识呢，本文就Kylin得基本概念和原理进行简述。

Kylin基本概念

首先想到的学习路径是Kylin官网： http://kylin.apache.org/cn/

给出的概念是： Apache Kylin™是一个开源的分布式分析引擎，提供Hadoop/Spark之上的SQL查询接口及多维分析（OLAP）能力以支持超大规模数据，最初由eBay Inc. 开发并贡献至开源社区。它能在亚秒内查询巨大的Hive表。

由Kylin的概念可以得出：

1. Kylin是一个国产的处理hadoop、spark等超大规模数据的一种分布式引擎

2. Kylin 是基于OLAP的

3. Kylin的速度非常快，亚秒级别可以在超大规模数据完成数据查询操作（亚秒也就是比1秒要慢一点点，大约1.2秒这样）

什么是OLAP？

OLAP： On-Line Analytic Processing 联机分析处理，分为：

MOLAP : Multi-Dimensional OLAP  kylin是一个MOLAP系统，通过预计算的方式缓存了所有需要查询的的数据结果，需要大量的存储空间（原数据量的10+倍）。

ROLAP: Relational OLAP   Mondrian是一个ROLAP系统，所有的查询可以通过实时的数据库查询完成，而不会有任何的预计算，大大节约了存储空间的要求（但是会有查询结果的缓存，目前是缓存在程序内存中，很容易导致OOM

HOLAP: Hybrid OLAP  混合型的OLAP。

为什么Kylin 能够实现超大数据的亚秒级查询？

官网给出的解答是：

Apache Kylin™令使用者仅需三步，即可实现超大数据集上的亚秒级查询。

1 定义数据集上的一个星形或雪花形模型

2 在定义的数据表上构建cube

3 使用标准SQL通过ODBC、JDBC或RESTFUL API进行查询，仅需亚秒级响应时间即可获得查询结果

顺藤摸瓜，那么什么是Kylin 星形、雪花模型呢？

星型模型：

有一张事实表、以及零个或多个维度表；事实表与维度表通过 主键/外键 相关联，维度表之间没有关联，就像很多星星围绕在一个恒星周围，顾命名为星型模型。

雪花模型：

如果将星型模型中某些维度的表再做规范，抽取成更细的维度表，然后让维度表之间也进行关联，那么这种模型成为雪花模型（雪花模型可以通过一定的转换，变为星型模型）

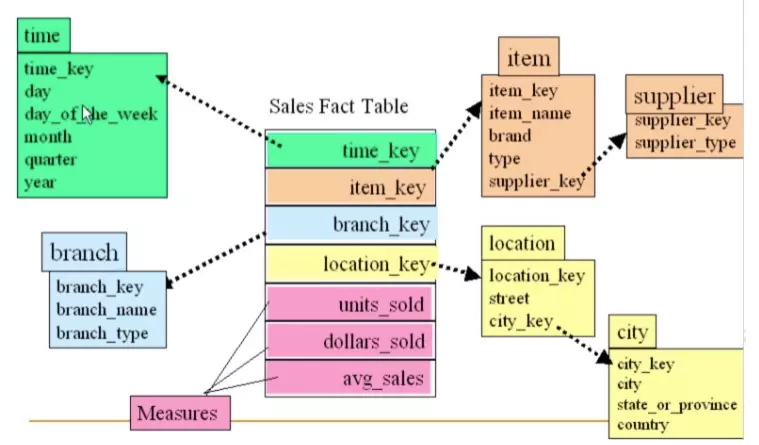
如何构建Cube

Cube 即多维立方体，也叫数据立方体。如下图所示，这是由三个维度（维度数可以超过3个，下图仅为了方便画图表达）构成的一个OLAP立方体，立方体中包含了满足条件的cell(子立方块)值，这些cell里面包含了要分析的数据，称之为度量值。

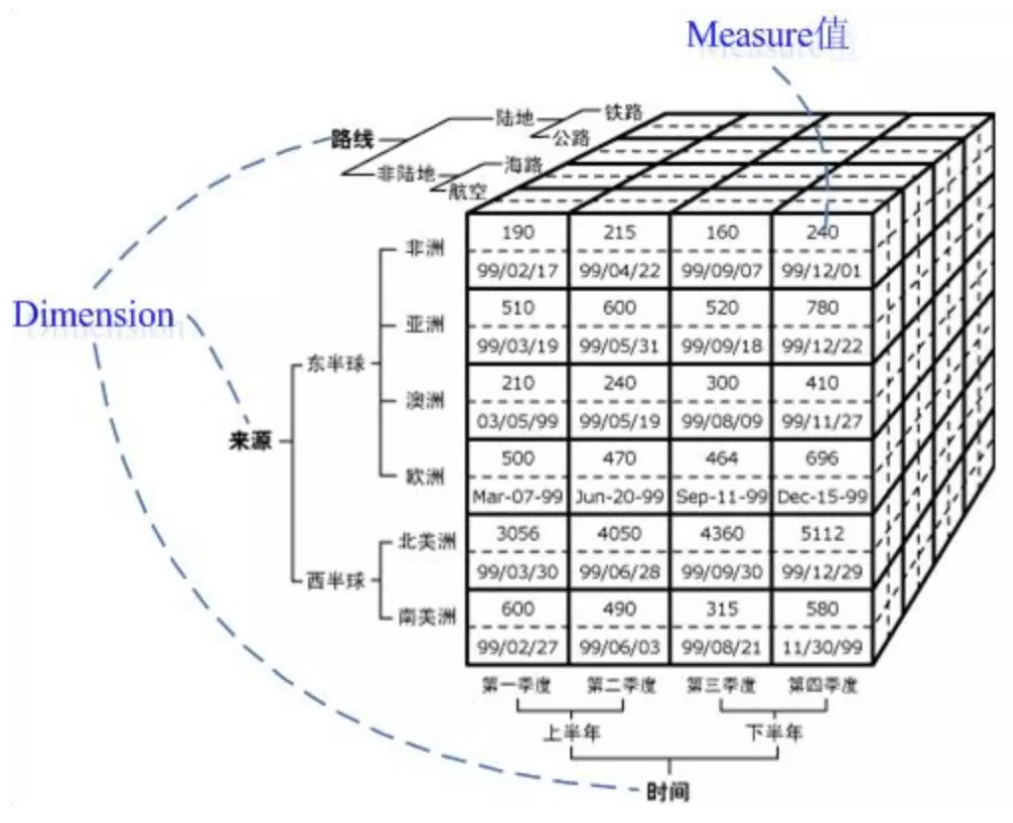
Cube：由维度构建出来的多维空间，包含了所有要分析的基础数据，所有的聚合数据操作都在立方体上进行

Dimension：观察数据的角度。一般是一组离散的值，比如：

• • 时间维度上的每一个独立的日期
  • 商品维度上的每一件独立的商品

Measure：即聚合计算的结果，一般是连续的值，比如：

• • 销售额，销售均价
  • 销售商品的总件数

事实表：是指存储有事实记录（明细数据）的表，如系统日志、销售记录等；事实表的记录在不断地动态增长，数据量大

维度表（维表）：保存了维度值，可以跟事实表做关联。常见的维度表如：

• • 日期表
  • 地点表
  • 分类表

Cuboid：对于每一种维度的组合，将度量做聚合运算，然后将运算的结果保存为一个物化视图，称为 Cuboid (即为上图的最小立方体单元，这也是cube的基石)

　　　　思考：

　　　　一个 Cube 有（M+N）个维度，那么会有 2的(M+N)次方 个 Cuboid ---------注意Kylin里面有很多方法可以减少无效的Cuboid, 例如某个表里面包含了

　　　　国家--省--市--县城  ，那么其他的组合都是错误的，这类可以直接排除。

　　　　Kylin查询为什么快，就是因为这个Cuboid包含了用户想要查询的任何情况，计算复杂度是O(1)

举一个简单Cube 代码例子，它可以是一个Json (太长进行了部分删减):

{
  "name": "test_cube",
  "model_name": "test_model",     // 使用名为 model_test 的数据模型
  "description": "",
  "null_string": null,
  "dimensions": [                 // 维度，可以来自事实表或维度表
    {
      "name": "PART_DT",
      "table": "KYLIN_SALES",
      "column": "PART_DT",
      "derived": null
    },
    {
      "name": "_MAX_",
      "function": {
        "expression": "MAX",
        "parameter": {
          "type": "column",
          "value": "KYLIN_SALES.PRICE"
        },
        "returntype": "decimal(19,4)"
      }
    }
  ],
  "dictionaries": [],
  "rowkey": {                 // rowkey 配置，主要关注维度列在 rowkey 中的位置（谁先谁后）
    "rowkey_columns": [
      {
        "column": "KYLIN_SALES.PART_DT",
        "encoding": "date",
        "encoding_version": 1,
        "isShardBy": false
      },
      {
        "column": "KYLIN_CAL_DT.CAL_DT",
        "encoding": "date",
        "encoding_version": 1,
        "isShardBy": false
      }
    ]
  },
  "hbase_mapping": {
    "column_family": [
      {
        "name": "F1",
        "columns": [
          {
            "qualifier": "M",
            "measure_refs": [
              "_COUNT_",
              "_SUM_",
              "_MAX_"
            ]
          }
        ]
      }
    ]
  },
  "aggregation_groups": [     // aggregation groups 配置，共两个 aggregation groups
    {
      "includes": [
        "KYLIN_SALES.PART_DT",
        "KYLIN_SALES.LEAF_CATEG_ID",
        "KYLIN_SALES.LSTG_SITE_ID",
        "KYLIN_SALES.SLR_SEGMENT_CD",
        "KYLIN_SALES.OPS_USER_ID",
        "KYLIN_CAL_DT.CAL_DT"
      ],
      "select_rule": {
        "hierarchy_dims": [],
        "mandatory_dims": [],
        "joint_dims": []
      }
    }
  ],
  "partition_date_start": 0,            // Cube 日期/时间 分区起始值
  "partition_date_end": 3153600000000,  // Cube 日期/时间 分区结束值
  "auto_merge_time_ranges": [           // 自动合并小的 segments 到中等甚至更大的 segment
    604800000,
    2419200000
  ],
  "retention_range": 0,                 // 不删除旧的 Cube Segment
  "engine_type": 4,                     // 构建 Cube 的引擎为 Spark
  "storage_type": 2,                    // 使用 Hbase 存储 Cube
  "override_kylin_properties": {},
  "cuboid_black_list": []
}

至此，已经对Kylin的整体原理有一个初步的理解。

 

 

Kylin 的总体架构与特性

上图是Kylin官网给出的总体架构图，比较通俗易懂，它有如下特性:

 

1. 可扩展超快的基于大数据的OLAP引擎:

　　Kylin是为减少在Hadoop/Spark上百亿规模数据查询延迟而设计

2. 交互式查询能力:

　　通过Kylin，用户可以与Hadoop数据进行亚秒级交互，在同样的数据集上提供比Hive更好的性能

3. 实时 OLAP：

　　Kylin可以在数据产生时进行实时处理，用户可以在秒级延迟下进行实时数据的多维分析。

4. Hadoop ANSI SQL 接口:

　　作为一个OLAP引擎，Kylin为Hadoop提供标准SQL支持大部分查询功能

5. 多维立方体（MOLAP Cube）:

　　用户能够在Kylin里为百亿以上数据集定义数据模型并构建立方体

6. 与BI工具无缝整合:

　　Kylin提供与BI工具的整合能力，如Tableau，PowerBI/Excel，MSTR，QlikSense，Hue和SuperSet

7. 其他特性：

• Job管理与监控
• 压缩与编码
• 增量更新
• 利用HBase Coprocessor
• 基于HyperLogLog的Dinstinc Count近似算法
• 友好的web界面以管理，监控和使用立方体
• 项目及表级别的访问控制安全
• 支持LDAP、SSO

 

进一步的学习有如下资料可参考：

1. Kylin的实操构建：http://kylin.apache.org/cn/docs15/tutorial/create_cube.html             https://www.jianshu.com/p/93dccb6b62c5  

2. 本文参考了： https://www.jianshu.com/p/4f4417ef790a