【校内test】桶哥的问题

（以上题目出自_rqy两年前）

#A：桶哥的问题——买桶【链接】

【题目描述】

桶哥要买一些全家桶。他有a元钱，而每个桶要花b元钱。他能不能买到c个桶？

【输入格式】

一行三个整数a, b, c

【输出格式】

Yes或No

【输入样例#1】                    【输出样例#1】

26 4 5                                    Yes

【输入样例#2】                    【输出样例#2】

3 4 5                                        No

---

显然这道题很很很简单的了，然后数据好像也没有需要特判的（好像有些人特判然后就90pts了qwq）

思路就是直接b*c与a比，如果b*c≤a，那么Yes，否则No

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>

using namespace std;

long long a,b,c;//唯一注意要开long long

int main(){
    scanf("%lld%lld%lld",&a,&b,&c);
    long long ans = b*c;
    if(ans<=a)cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
    return ;
}

没什么大问题，next~

---

#B：桶哥的问题——送桶【链接】

【题目描述】

桶哥买了n个桶，他要将这些桶送去n个人的家。他送第i个桶需要a_i的时间，需要在b_i之前送到。桶哥很懒，他想要尽量晚起身去送桶。问他最晚什么时候要去送桶？

桶哥在送完一个桶之后可以紧接着去送另一个桶。

【输入格式】

一行一个整数n，以下n行每行两个整数表示a_i，b_i。

【输出格式】

一行一个整数，表示桶哥最晚什么时候起身。

【输入样例】                              【输出样例】

4                                                    2
1 6
2 7
2 8
1 7

---

40pts-错误思路：把所有a_i加起来sum_（ai），然后找到一个最大的b_i，用b_i（max）-sum_（ai）可以得40pts；

90pts-错误思路：计算每个ai与bi的差值，以及b_i（max）-sum_（ai），取min，可以骗到90pts；

100pts-正确思路：
对所有的桶按照bi的大小，从小到大排序（对于ai没有要求）（可以用sort解决），然后从1~n for循环：求出当前枚举到的所有ai的和suma，用当前的bi（因为已经排过序了所以当前bi即为当前最大的bi）减去suma（差值暂且叫它kb），取最小的kb即为ans；

90pts代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
const int maxn=1e6+;

using namespace std;

int n,minn=1e9+,suma,maxb;

struct tong{
    int a,b,c;
}t[maxn];

bool cmp(tong x,tong y){
    if(x.b==y.b)return x.a>y.a;
    else return x.b<y.b;
}

int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d%d",&t[i].a,&t[i].b);
        t[i].c=t[i].b-t[i].a;
        if(t[i].c<minn) minn = t[i].c;
        if(t[i].b>maxb)maxb=t[i].b;
        suma+=t[i].a;
    }
    int sumc=maxb-suma;
    if(sumc<minn)cout<<sumc<<endl;
    else cout<<minn<<endl;

    return ;
}

100pts代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
const int maxn=1e6+;

using namespace std;

int n,suma,kb,ans=1e9;

struct tong{
    int a,b,c;
}t[maxn];

bool cmp(tong x,tong y){
    if(x.b==y.b)return x.a>y.a;
    else return x.b<y.b;
}

int main(){

    scanf("%d",&n);
    for(int i=;i<=n;i++)
        scanf("%d%d",&t[i].a,&t[i].b);

    sort(t+,t+n+,cmp);

    for(int i=;i<=n;i++){
        suma+=t[i].a;
        kb=t[i].b-suma;
        if(kb<ans) ans=kb;
    }

    cout<<ans<<endl;

    return ;
}

---

#C：桶哥的问题——吃桶【链接】

【题目描述】

桶哥的桶没有送完，他还有n个桶。他决定把这些桶吃掉。他的每一个桶两个属性：种类ai和美味值bi。若下标为x，y，z（下标从1开始）的三个桶满足：

x<z且x+y=z-2y且a_x=a_z

那么它们构成一个套餐，会产生

（x+z）*（b_x-b_z）

的价值。问：一共会产生多少价值？

【输入格式】

第一行两个整数n，m，表示共有m种共n个桶。

第二行n个整数表示bi，

第三行n个整数表示ai。

【输出格式】

一行一个整数，表示一共会产生多少价值。由于这个数可能很大，你只需要输出它除以10007的余数。如果答案是负的，请将其加上10007再对10007取余。

【输入样例#1】                【输出样例#1】

5 2                                       23
6 7 8 7 3
1 2 2 1 2

【输入样例#2】                 【输入样例#2】

5 2                                        9974
6 3 8 7 7
1 2 2 1 2

_{【数据范围】（是个谜）}

---

40~50pts思路：

直接暴力模拟这个过程，时间复杂度大概是O（n² ）的

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
const int maxn=;
const int mo=;

using namespace std;

int n,m,xb,ans;

struct jgt{
    int a,b,xb;
}t[maxn];

int main(){
    scanf("%d%d",&n,&m);

    for(int i=;i<=n;i++)
      scanf("%d",&t[i].b);

    for(int i=;i<=n;i++)
      scanf("%d",&t[i].a);

    for(int i=;i<=n;i++){
        for(int j=;j<=n;j++){
            xb=i+j*;
            if(t[xb].a==t[i].a) ans += ((i+xb)%mo*(t[i].b-t[xb].b)%mo)%mo;
            else continue;
        }
    }
    ans%=mo;ans+=mo;ans%=mo;
    cout<<ans<<endl;
}

100pts：

化简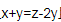介个式子，可以知道x与z mod3 同余。那么我们可以不管y了，将这n个桶分为下标mod3余1，mod3余2和mod3余0三种，那么对于组来说：

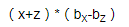
这个式子可以拆成xb_x+zb_x-xb_z-zb_z

对于每一项分开枚举：

xb_x：

开两个数组：c1[]和c[]，c1[i]用来储存第i种桶的xb_x是多少，c[i]用来储存当前枚举到的所有的第i种桶的xbx的和（每个xbx只加一遍）

那么有：

        c1[t[i].a] = (c1[t[i].a]%mod+c[t[i].a]%mod);//存储xbx
        //举个例子：假设mod3余1的有：（下标，种类，价值）(1,1,6)(4,1,7)(7,1,2),
          那么第一遍：c1[1]=0+0=0；c[1]=0+1*6=6第二遍：
c1[]=+=；c[]=+*=;第三遍:c1[]=+;c[]=+；
这样刚好每个x都加了对应的遍数
        c[t[i].a] = (c[t[i].a]%mod+(i%mod)*(t[i].b%mod))%mod;

//用来存储xbx的一遍和。另外要注意把c1放在前面而不是c。

zb_x：

开两个数组：c2[]和c0[]，c2[i]用来储存第i种桶的zbx是多少，c0[i]用来储存当前枚举到的所有的第i种桶的bx和；

（啊我的天不知道怎么表达qwq）

    c2[t[i].a] = (c2[t[i].a]%mod+(i%mod)*(c0[t[i].a])%mod)%mod;//储存zbx
        c0[t[i].a] = (c0[t[i].a]%mod+t[i].b)%mod;//用于计算zbx时，储存bx

xb_z：

开两个数组：c4[]和c3[]，c4[i]用来储存第i种桶的xbz是多少，c3[i]用来储存当前枚举到的所有的第i种桶的下标和；

    c4[t[i].a] = (c4[t[i].a]%mod+c3[t[i].a]%mod*t[i].b%mod)%mod;//存储xbz
        c3[t[i].a] = c3[t[i].a]%mod+i%mod;//存储下标的和，用于计算xbz 

zb_z：

开两个数组：c6[]和c5[]，c6[i]用来储存第i种桶的zbz是多少，c5[i]用来储存当前枚举到的所有的第i种桶的个数；

  c6[t[i].a] = (c6[t[i].a]%mod+t[i].b%mod*c5[t[i].a]%mod*i%mod)%mod;//储存zbz
        c5[t[i].a] ++;//记录第i种桶个数

嗯-大概吧：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;

int read() {
  int ans = , c, f = ;
  while (!isdigit(c = getchar()))
    if (c == '-') f *= -;
  do ans = ans *  + c - '';
  while (isdigit(c = getchar()));
  return ans * f;
}

const int mod=;
const int maxn=;
int n,m,ans,ans1;
int c[maxn>>], c1[maxn>>], c2[maxn>>], c3[maxn>>],c0[maxn>>],c4[maxn>>];
int c5[maxn>>],c6[maxn>>];
struct jgt{
    int a,b;
}t[maxn];

int main(){

    scanf("%d%d",&n,&m);

    for(int i=;i<=n;i++)
        scanf("%d",&t[i].b),t[i].b%=mod;

    for(int i=;i<=n;i++)
        scanf("%d",&t[i].a);

    for(int i=;i<=n;i+=){
        c1[t[i].a] = (c1[t[i].a]%mod+c[t[i].a]%mod);//存储xbx
        c[t[i].a] = (c[t[i].a]%mod+(i%mod)*(t[i].b%mod))%mod;//用来存储xbx的一遍和
        c2[t[i].a] = (c2[t[i].a]%mod+(i%mod)*(c0[t[i].a])%mod)%mod;//储存zbx
        c0[t[i].a] = (c0[t[i].a]%mod+t[i].b)%mod;//用于计算zbx时，储存bx
        c4[t[i].a] = (c4[t[i].a]%mod+c3[t[i].a]%mod*t[i].b%mod)%mod;//存储xbz
        c3[t[i].a] = c3[t[i].a]%mod+i%mod;//存储下标的和，用于计算xbz
        c6[t[i].a] = (c6[t[i].a]%mod+t[i].b%mod*c5[t[i].a]%mod*i%mod)%mod;
        c5[t[i].a] ++;
    }

    for(int i=;i<=m;i++)
    ans = (ans%mod+c1[i]%mod+c2[i]%mod-c4[i]-c6[i])%mod;

    memset(c, , sizeof(c));memset(c0, , sizeof(c0));
    memset(c1, , sizeof(c1));memset(c2, , sizeof(c2));
    memset(c4, , sizeof(c4));memset(c3, , sizeof(c3));
    memset(c5, , sizeof(c5));memset(c6, , sizeof(c6));

    for(int i=;i<=n;i+=){
        c1[t[i].a] = (c1[t[i].a]%mod+c[t[i].a]%mod);//存储xbx
        c[t[i].a] = (c[t[i].a]%mod+(i%mod)*(t[i].b%mod))%mod;//用来存储xbx的一遍和
        c2[t[i].a] = (c2[t[i].a]%mod+(i%mod)*(c0[t[i].a])%mod)%mod;//储存zbx
        c0[t[i].a] = (c0[t[i].a]%mod+t[i].b)%mod;//用于计算zbx时，储存bx
        c4[t[i].a] = (c4[t[i].a]%mod+c3[t[i].a]%mod*t[i].b%mod)%mod;//存储xbz
        c3[t[i].a] = c3[t[i].a]%mod+i%mod;//存储下标的和，用于计算xbz
        c6[t[i].a] = (c6[t[i].a]%mod+t[i].b%mod*c5[t[i].a]%mod*i%mod)%mod;
        c5[t[i].a] ++;
    }

    for(int i=;i<=m;i++)
    ans = (ans%mod+c1[i]%mod+c2[i]%mod-c4[i]-c6[i])%mod;

    memset(c, , sizeof(c));memset(c0, , sizeof(c0));
    memset(c1, , sizeof(c1));memset(c2, , sizeof(c2));
    memset(c4, , sizeof(c4));memset(c3, , sizeof(c3));
    memset(c5, , sizeof(c5));memset(c6, , sizeof(c6));

    for(int i=;i<=n;i+=){
        c1[t[i].a] = (c1[t[i].a]%mod+c[t[i].a]%mod);//存储xbx
        c[t[i].a] = (c[t[i].a]%mod+(i%mod)*(t[i].b%mod))%mod;//用来存储xbx的一遍和
        c2[t[i].a] = (c2[t[i].a]%mod+(i%mod)*(c0[t[i].a])%mod)%mod;//储存zbx
        c0[t[i].a] = (c0[t[i].a]%mod+t[i].b)%mod;//用于计算zbx时，储存bx
        c4[t[i].a] = (c4[t[i].a]%mod+c3[t[i].a]%mod*t[i].b%mod)%mod;//存储xbz
        c3[t[i].a] = c3[t[i].a]%mod+i%mod;//存储下标的和，用于计算xbz
        c6[t[i].a] = (c6[t[i].a]%mod+t[i].b%mod*c5[t[i].a]%mod*i%mod)%mod;
        c5[t[i].a] ++;
    }

    for(int i=;i<=m;i++)
    ans = (ans%mod+c1[i]%mod+c2[i]%mod-c4[i]-c6[i])%mod;

    printf("%d",(ans+mod)%mod);

  }

最后，一定要记得：多取模

败在了取mod取得少上qwq

end-