一本通&&洛谷 ——靶型数独——题解

题目传送

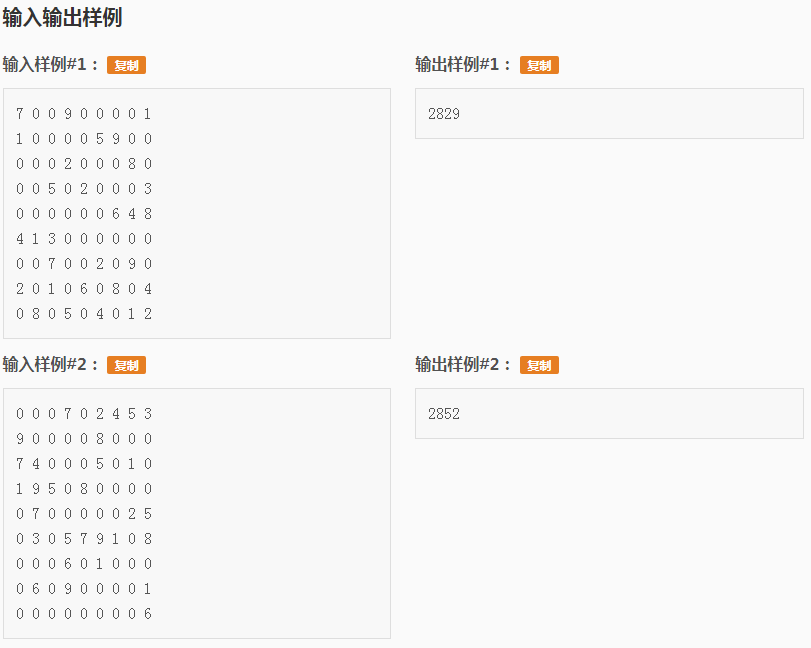
主要是搜索顺序不同导致效率千差万别。

联想人做数独的策略，总是先填可填数最少的那个空，再填选择第二少的。。。其实这种策略就造就了一个深度浅时分支也较少的搜索树。合适的搜索顺序再配合剪枝==AC。

所以搜索顺序为：从当前可填数的数目最少的那个空开始。注意：每填一个空，都会导致同行同列同九宫格的空的可填数数目减一，所以不能一开始就排序。（实测这样做会比正解慢8倍左右，真是恐怖如斯）所以要在分支选择时去找。为了平衡准确性与高效性，可以用一个简单的判断找到一个比较合适的空去填（因为如果每次都精确去找那个可填数数目最小的那个空会导致复杂度偏高，因此只要简单地找到可填数数目相对小的那个空就行）。

找一下搜索面临或有关的状态与维度：当前分数v，当前要填的点的坐标，填了t个点，总共要填cnt个点，各行各列各九宫格填数情况。

可行性剪枝考虑：

　　发现一个有趣的性质：数独中每一行都会有1到9各出现一次，共有9行，所以1到9每个数到最后必定出现9次，所以可以设一个used[]数组记录数出现的次数，若小于0，肯定不是正解，回溯，故每次填空要用不仅usedi大于0且i在同行同列同九宫格都没有出现过的i。

最优性剪枝：

　　可以将所有空能填的最大的数*该空的分数求和得到一个还能得到的至多的分数zhiduo，填空时，若发现v+zhiduo还<=已搜到的答案ans，显然不会使答案更优，所以回溯；同时每填一个空都更新一下zhiduo，回溯时也要照顾到zhiduo。

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>

 using namespace std;

 int a[][],fen[][],cnt,zhiduo,m[][],ans;//第二下标：  0：纵坐标；1：横坐标   先纵再横
 int ma[][],used[];
 int h[],l[],maxh,maxl;//某行、列已经填了几个数 

 bool hang[][],lie[][],jiu[][][];//行、列、九宫格的填数情况 

 void init()
 {
     for(int i=;i<=;i++) used[i]=;
     for(int f=;f<=;f++)//初始化每个空的分数，不懂的可以拿纸笔自己模拟一下
     {
         for(int i=f-;i<=-f+;i++) fen[f-][i]=fen[-f+][i]=f;
         for(int j=f-+;j<=-f+-;j++) fen[j][f-]=fen[j][-f+]=f;
     }
 }

 void dfs(int k,int v,int x,int y)//要填第k个，当前分数v，当前填的空的纵、横坐标。
 {
     if(v+zhiduo<=ans) return;//最优性剪枝
     for(int i=;i<=;i++)//填哪个数
     {
         if(used[i]&&(!hang[x][i])&&(!lie[y][i])&&(!jiu[x/][y/][i]))//可行性剪枝
         {
             v+=fen[x][y]*i;
             if(k!=cnt)
             {
                 used[i]--;
                 hang[x][i]=;lie[y][i]=;jiu[x/][y/][i]=;
                 h[x]++;l[y]++;
                 zhiduo-=fen[x][y]*ma[x][y];
                 maxh=maxl=;
                 a[x][y]=i;
                 for(int i=;i<=;i++)    if(h[i]!=&&h[i]>h[maxh]) maxh=i;//找接下来要填的空
                 for(int i=;i<=;i++)   if(!a[maxh][i]&&l[i]!=&&l[i]>l[maxl]) maxl=i;
                 dfs(k+,v,maxh,maxl);
                 hang[x][i]=;lie[y][i]=;jiu[x/][y/][i]=;//回溯的时候少一个都会wa啊
                 zhiduo+=fen[x][y]*ma[x][y];
                 h[x]--;l[y]--;
                 a[x][y]=;
                 used[i]++;
             }
             else
                 ans=max(ans,v);
             v-=fen[x][y]*i;
         }
     }
 }

 int main()
 {
     init();
     int v=;
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
         {
             scanf("%d",&a[i][j]);
             if(a[i][j])
             {
                 used[a[i][j]]--;
                  h[i]++;
                  l[j]++;
                 if(hang[i][a[i][j]]||lie[j][a[i][j]]||jiu[i/][j/][a[i][j]])
                 {
                     cout<<-;
                     return ;
                 }
                 hang[i][a[i][j]]=;
                 lie[j][a[i][j]]=;
                 jiu[i/][j/][a[i][j]]=;
                 v+=fen[i][j]*a[i][j];
             }
             else
                 cnt++;
         }
     int most;
     for(int i=;i<=;i++)//求起始时的至多zhiduo
         for(int j=;j<=;j++)
         if(!a[i][j])
         {
             most=;
             while(hang[i][most]||lie[j][most]||jiu[i/][j/][most]) most--;
             ma[i][j]=most;//空（j,i）能填的最大的数
             zhiduo+=most*fen[i][j];
         }
     h[]=-;
     l[]=-;
     maxh=,maxl=;
     for(int i=;i<=;i++)//找一开始要填的空
         if(h[i]!=&&h[i]>h[maxh]) maxh=i;
     for(int i=;i<=;i++)
         if(!a[maxh][i]&&l[i]!=&&l[i]>l[maxl]) maxl=i;
     dfs(,v,maxh,maxl);
     if(!ans) ans=-;
     cout<<ans;
     return ;
 }