BZOJ4625 [BJOI2016]水晶 最小割

题意简述

给你一个三维的坐标系，坐标系上 \((x_i+y_i+z_i)\bmod 3 = 0\) 的点内有能量源。给定 \(n\) 个点含有能量值为 \(c_i\) 的水晶，如果一个水晶位于能量源上，这个水晶的能量值将会提高 \(10\%\)。

水晶有两种共振情况，一是相邻的三个水晶共振，二是两个水晶在一条长度为 \(2\) 的线段两端，且线段中点是能量源。

你可以炸掉一些水晶，请问没有共振之后剩余水晶的最大能量值。

做法

对于 \((x_i+y_i+z_i)\bmod 3 \not = 0\) 的点黑白染色，如果一个能量源的周围同时存在黑白两种颜色的点，那么必定构成共振，如图所示

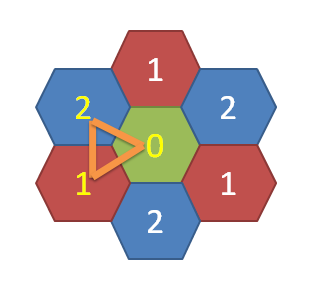
于是我们可以把 \(\bmod 3\) 意义下的三种点分别拆点。考虑对于每个共振，要用最小代价破坏，显然是一个最小割的模型。把每个点拆点，边权为水晶的能量值 \(c_i\) 。然后源点连 \(1\) 的点，\(1\) 连 \(0\)，\(0\) 连 \(2\)，\(2\) 连 汇点，答案为水晶的总能量 \(\sum c_i\) 减最大流。这里给出代码实现：

const int inf=1e9;
inline void link(int a,int b,int c)
{
	add_edge(S,a<<1,inf);add_edge(a<<1|1,b<<1,inf);
	add_edge(b<<1|1,c<<1,inf);add_edge(c<<1|1,T,inf);
}

然后我们用一个结构体来表示每一个点，将\((x_i,y_i,z_i)\)转换为\((x_i-z_i,y_i-z_i)\)，用一个向量的结构体来封存，重载<和+预算符，用一个map来对向量进行操作，本题就结束了。

代码实现

map常数大跑不快，但是很好写。

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define ak *
#define in inline
#define db double
in char getch()
{
	static char buf[1<<12],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<12,stdin),p1==p2)?EOF:*p1++;
}
char qwq;
#define gc() getchar()
in int read()
{
	re cz=0,ioi=1;qwq=gc();
	while(qwq<'0'||qwq>'9') ioi=qwq=='-'?~ioi+1:1,qwq=gc();
	while(qwq>='0'&&qwq<='9') cz=(cz<<3)+(cz<<1)+(qwq^48),qwq=gc();
	return cz ak ioi;
}
const int N=5e4+5,inf=1e9;
int n,m,h[N<<1],cnt=1,dis[N<<1],s,t,q[N<<1],l,r,cur[N<<1],tot,sum;
struct did{int next,to,f;}e[N*20];
in void add(re x,re y,re z)
{
	e[++cnt]=(did){h[x],y,z},h[x]=cnt;
	e[++cnt]=(did){h[y],x,0},h[y]=cnt;
}
const db eps=1e-9;
inline int bfs(re u)
{
	memset(dis,-1,sizeof(dis));dis[u]=0;
	l=r=0;q[++r]=u;
	while(l<r)
	{
		re i=q[++l]; if(i==t) return 1;
		for(re j=h[i],k;k=e[j].to,j;j=e[j].next)
		if(dis[k]<0&&e[j].f) dis[k]=dis[i]+1,q[++r]=k;
	}
	return 0;
}
in int dfs(re u,re maxf)
{
	re res=0;
	if(u==t||!maxf) return maxf;
	for(re &i=cur[u],v;v=e[i].to,i;i=e[i].next)
	if(e[i].f&&dis[v]==dis[u]+1)
	{
		re delta=dfs(v,min(maxf,e[i].f));
		e[i].f-=delta;e[i^1].f+=delta;
		res+=delta;maxf-=delta;
		if(!maxf) return res;
	}
	if (fabs(maxf-res)<eps) dis[u]=-2;
	return res;
}
inline int dinic()
{
	re ans=0;
	while(bfs(s)) memcpy(cur,h,sizeof(h)),ans+=dfs(s,inf);
	return ans;
}
struct poi //poipoi qwq~
{
	int x,y;
	poi (re a=0,re b=0) {x=a,y=b;}
	in bool operator < (poi a) const {return x==a.x?y<a.y:x<a.x;}
	in poi operator + (poi a) const {return poi(x+a.x,y+a.y);}
}p[N];
map<poi,int>mp,ext,f,book;
in void link(re a,re b,re c)
{
	if(!book[poi(s,a)]) add(s,a<<1,inf),book[poi(1,a)]=1;
	if(!book[poi(a,b)]) add(a<<1|1,b<<1,inf),book[poi(a,b)]=1;
	if(!book[poi(b,c)]) add(b<<1|1,c<<1,inf),book[poi(b,c)]=1;
	if(!book[poi(c,t)]) add(c<<1|1,t,inf),book[poi(c,a)]=1;
}
int main()
{
	n=read();
	for(re i=1;i<=n;i++)
	{
		re x=read(),y=read(),z=read(),c=read();
		p[i]=poi(x-z,y-z);if(!ext[p[i]]) ext[p[i]]=++tot;
		mp[p[i]]+=c;f[p[i]]=((x+y+z)%3==0);
	}
	s=1,t=tot+1<<1;
	for(re i=1;i<=n;i++) if(f[p[i]]<2)
	{
		re pt=ext[p[i]],ene=mp[p[i]]*(10+f[p[i]]);sum+=ene;
		add(2*pt,2*pt+1,ene);if(!f[p[i]]) {f[p[i]]=2;continue;}
		static int a[N],b[N];re na=0,nb=0;f[p[i]]=2;
		if(!(a[++na]=ext[p[i]+poi(0,1)])) na--;
		if(!(a[++na]=ext[p[i]+poi(1,0)])) na--;
		if(!(a[++na]=ext[p[i]+poi(-1,-1)])) na--;
		if(!(b[++nb]=ext[p[i]+poi(0,-1)])) nb--;
		if(!(b[++nb]=ext[p[i]+poi(-1,0)])) nb--;
		if(!(b[++nb]=ext[p[i]+poi(1,1)])) nb--;
		for(re x=1;x<=na;x++)
		for(re y=1;y<=nb;y++)
		link(a[x],pt,b[y]);
	}
	printf("%.1lf",(db)(sum-dinic())/10);
	return 0;
}