6389. 【NOIP2019模拟2019.10.26】小w学图论

题目描述

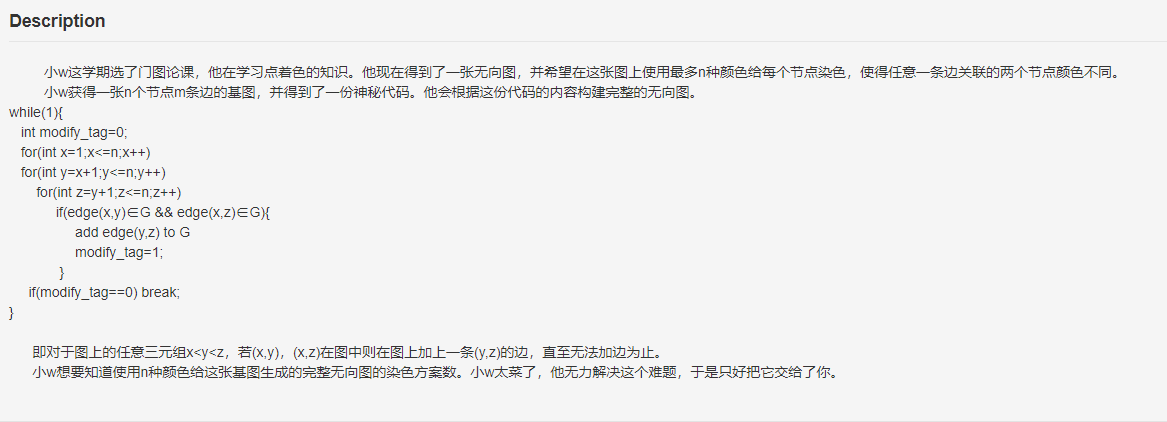
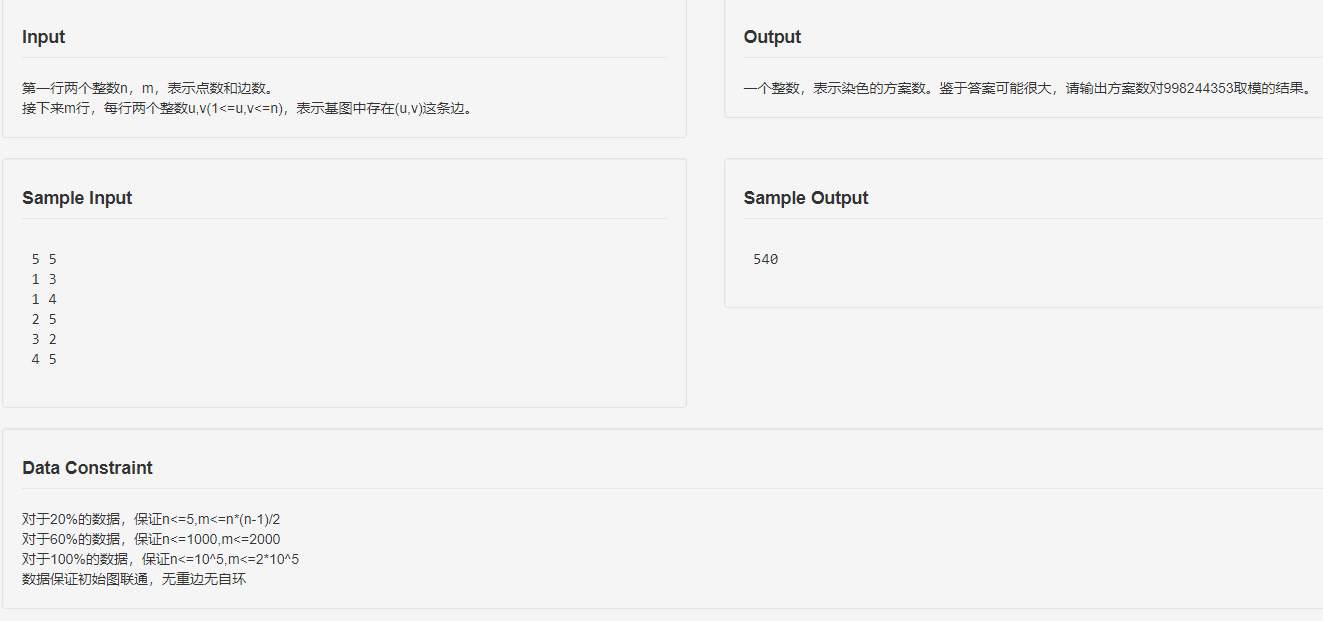
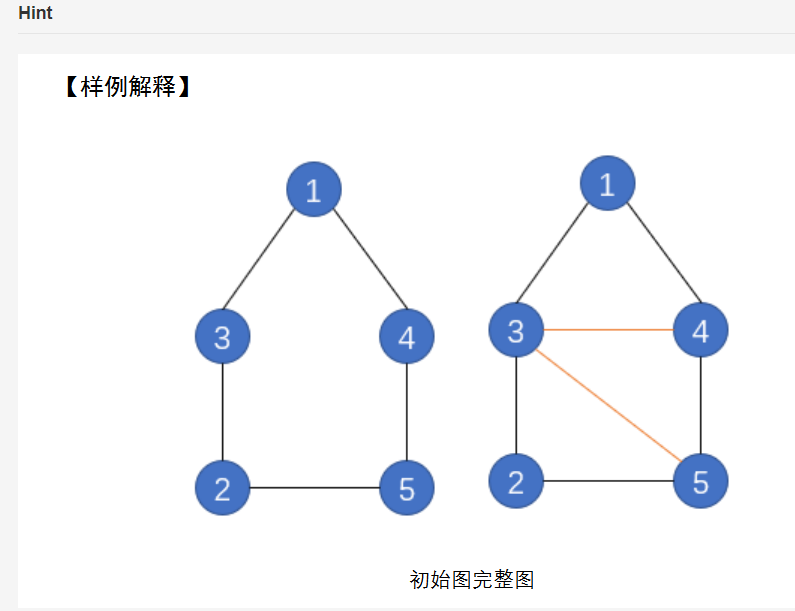
题解

之前做过一次

假设图建好了，设g[i]表示i->j（i<j）的个数

那么ans=∏(n-g[i])，因为连出去的必定会构成一个完全图，颜色互不相同

从n~1染色，点i的方案数是(n-g[i])

用线段树合并维护集合即可

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define mod 998244353
using namespace std;
int tr[4000001][4];
int n,m,i,j,k,l,x,y,len;
long long ans,sum;
void swap(int &x,int &y)
{
	int z=x;
	x=y;
	y=z;
}
void New(int t,int x)
{
	if (!tr[t][x])
	{
		tr[t][x]=++len;
		tr[len][3]=n+1;
	}
}
void change(int t,int l,int r,int x)
{
	int mid=(l+r)/2;
	++tr[t][2];
	tr[t][3]=min(tr[t][3],x);
	if (l==r)
	return;
	if (x<=mid)
	{
		New(t,0);
		change(tr[t][0],l,mid,x);
	}
	else
	{
		New(t,1);
		change(tr[t][1],mid+1,r,x);
	}
}
int find(int t,int l,int r,int x,int y)
{
	int sum=0,mid=(l+r)/2;
	if (x<=l && r<=y)
	return tr[t][2];
	if (x<=mid)
	{
		if (tr[t][0])
		sum+=find(tr[t][0],l,mid,x,y);
	}
	if (mid<y)
	{
		if (tr[t][1])
		sum+=find(tr[t][1],mid+1,r,x,y);
	}
	return sum;
}
int Find(int t,int l,int r,int x)
{
	int mid=(l+r)/2,ans=n+1,s;
	if (x<=l) return tr[t][3];
	if (tr[t][0] && x<=mid)
	s=Find(tr[t][0],l,mid,x),ans=min(ans,s);
	if (tr[t][1])
	s=Find(tr[t][1],mid+1,r,x),ans=min(ans,s);
	return ans;
}
void merge(int t1,int t2,int l,int r)
{
	int mid=(l+r)/2;
	if (l==r) return;
	if (tr[t1][0] && tr[t2][0])
	merge(tr[t1][0],tr[t2][0],l,mid);
	else
	if (tr[t2][0])
	tr[t1][0]=tr[t2][0];
	if (tr[t1][1] && tr[t2][1])
	merge(tr[t1][1],tr[t2][1],mid+1,r);
	else
	if (tr[t2][1])
	tr[t1][1]=tr[t2][1];
	tr[t1][2]=tr[tr[t1][0]][2]+tr[tr[t1][1]][2];
	tr[t1][3]=min(tr[tr[t1][0]][3],tr[tr[t1][1]][3]);
}
int main()
{
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	scanf("%d%d",&n,&m);
	len=n;
	fo(i,1,n)
	tr[i][3]=n+1;
	fo(i,1,m)
	{
		scanf("%d%d",&x,&y);
		if (x>y) swap(x,y);
		change(x,1,n,y);
	}
	tr[0][3]=n+1;
	ans=n;
	fo(i,1,n-1)
	{
		ans=(ans*(n-find(i,1,n,i+1,n)))%mod;
		j=Find(i,1,n,i+1);
		if (j<=n)
		merge(j,i,1,n);
	}
	printf("%lld\n",ans);
	fclose(stdin);
	fclose(stdout);
	return 0;
}