非线性优化-NLopt

通过 对 一个 数学 模型 的求解 来介绍 NLopt的使用方法

数学模型：

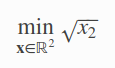
这个是目标函数 求满足 条件的情况下 x2的开平方最小

边界约束

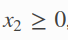
非线性不等式约束如下

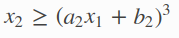
有两个参数 x1 和 x2 ，其中 a和b是模型的参数可以设为任意的固定值，这个模型设为a1=2，b1=0，a2=-1，b2=1

绘制这两条曲线 如下图

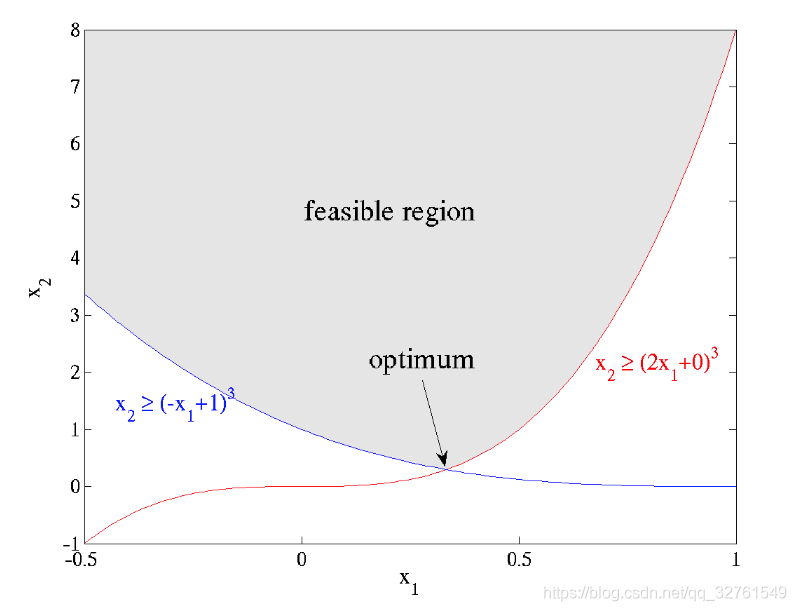
可行性区域在交汇的上方，最优点在交汇处，最优值大约为0.5443

下面通过NLopt的方式来求解这个数学模型。

通过图片上的曲线可以看出，x2>0的约束没有什么用，因为可行性区域的都在0之上

但是在使用NLopt的时候最好也把这个条件加上去。

nlopt.cc

#include <nlopt.hpp>
#include <iostream>
#include <math.h>
using namespace std;
int count = 0;
typedef struct {
    double a, b;
} my_constraint_data;
double myfunc(const std::vector<double>& x, std::vector<double>& grad, void *my_func_data)
{

    count++;
    if(!grad.empty())
    {
        grad[0] = 0.0;
        grad[1] = 0.5 / sqrt(x[1]);
    }
    return sqrt(x[1]);
}

double myconstraint(const std::vector<double>& x, std::vector<double>& grad, void *data)
{
    //声明对应外部数据刚定义的结构体 数据 然后赋值就可以了
    my_constraint_data *d = (my_constraint_data *) data;
    //获得a和b
    double a = d->a, b = d->b;
    if(!grad.empty())
    {
        grad[0] = 3 * a * (a*x[0] + b) * (a*x[0] + b);//对x0求偏导
        grad[1] = -1.0;//对x1求偏导
    }
    return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]);//返回 不等函数
 }

int main()
{
    my_constraint_data data[2] = { {2,0}, {-1,1} };//不等式的外部参数  上面定义的结构体
    nlopt::opt opt(nlopt::LD_SLSQP, 2);
    opt.set_min_objective(myfunc, NULL);
    opt.add_inequality_constraint(myconstraint, &data[0], 1e-8);
    opt.add_inequality_constraint(myconstraint, &data[1], 1e-8);
    opt.set_xtol_rel(1e-4);
        /*优化参数的边界约束*/
    std::vector<double> lb {0.1,0.1};//注意参数的个数要对应上
    std::vector<double> ub {10000,10000};//注意参数的个数要对应上
        //设置 参数 边界
    opt.set_lower_bounds(lb);//设置参数下限
    opt.set_upper_bounds(ub);//设置参数上限

    std::vector<double> x(2);
    x[0] = 2.5;
    x[1] = 4.3;
    double minf;

    std::cout << "start optimize" << std::endl;
    nlopt::result result = opt.optimize(x, minf);
    std::cout << "count:" << count << endl;
    std::cout << "found minimum at x1:" << x[0] << "x2:" << x[1] << "minf:" << minf << std::endl;

    return 0;
}

CMakeLists.txt

cmake_minimum_required(VERSION 2.8.3)
project(nloptDemo)

find_package(Eigen3 REQUIRED)

find_package(
  nlopt
)

include_directories(
    ${Eigen3_INCLUDE_DIRS}
    ${nlopt_INCLUDE_DIRS}
)

link_directories(${nlopt_LIBARIES})
add_definitions(${nlopt_DEFINITIONS})

set(CMAKE_CXX_FLAGS "-std=c++11 ${CMAKE_CXX_FLAGS} -O0 -Wall")

add_executable(nloptDemo nlopt.cc)
target_link_libraries( nloptDemo
    ${nlopt_LIBRARIES}
    )  

运行结果：

start optimize
count:9
found minimum at x1:0.333333x2:0.296296minf:0.544331

经过实验，发现初值对程序运行比较重要