Kronecker convolution 克罗内克卷积理解

在了解空洞卷积时候发现了Kronecker convolution是对空洞卷积的改进，于是学习了一下 ，原文连接：1812.04945v1.pdf (arxiv.org) 个人理解如下：

　　首先，对于一个普通卷积，假设输入为A，A的大小为(Ha,Wa,Ca)，卷积后的输出为B，B的大小为(Hb,Wb,Cb)，卷积核 K 的大小为Cb*Ca*(2k+1)(2k+1)。

　　对于所提出的Kronecker卷积，引入了一个变换矩阵 F ，通过F与K的乘积来扩展K，K经过扩展后记为K‘，K‘的大小为r1(2k+1)*r1(2k+1)。相应地，A中参与卷积的Patch大小也就从原来的(2k+1)(2k+1)变成了(2k+1)r1*(2k+1)r1。其中F由单位矩阵和0矩阵组成，大小为r1*r1，r1被称为内部膨胀因子，用来控制卷积核的膨胀率。r2为内部共享因子，控制子区域的大小。

也就是说 与单纯插入0的空洞卷积相比，Kronecker卷积通过与变换矩阵F的乘积展开核，内部膨胀因子控制核的膨胀率，内部共享因子控制子区域的大小。

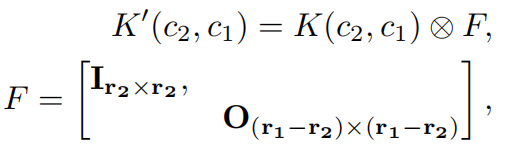
那么为什么F与K相乘后K的大小增大了呢？

　　这是因为F与K的相乘方法为 Kronecker product ，即克罗内克积，其定义如下：

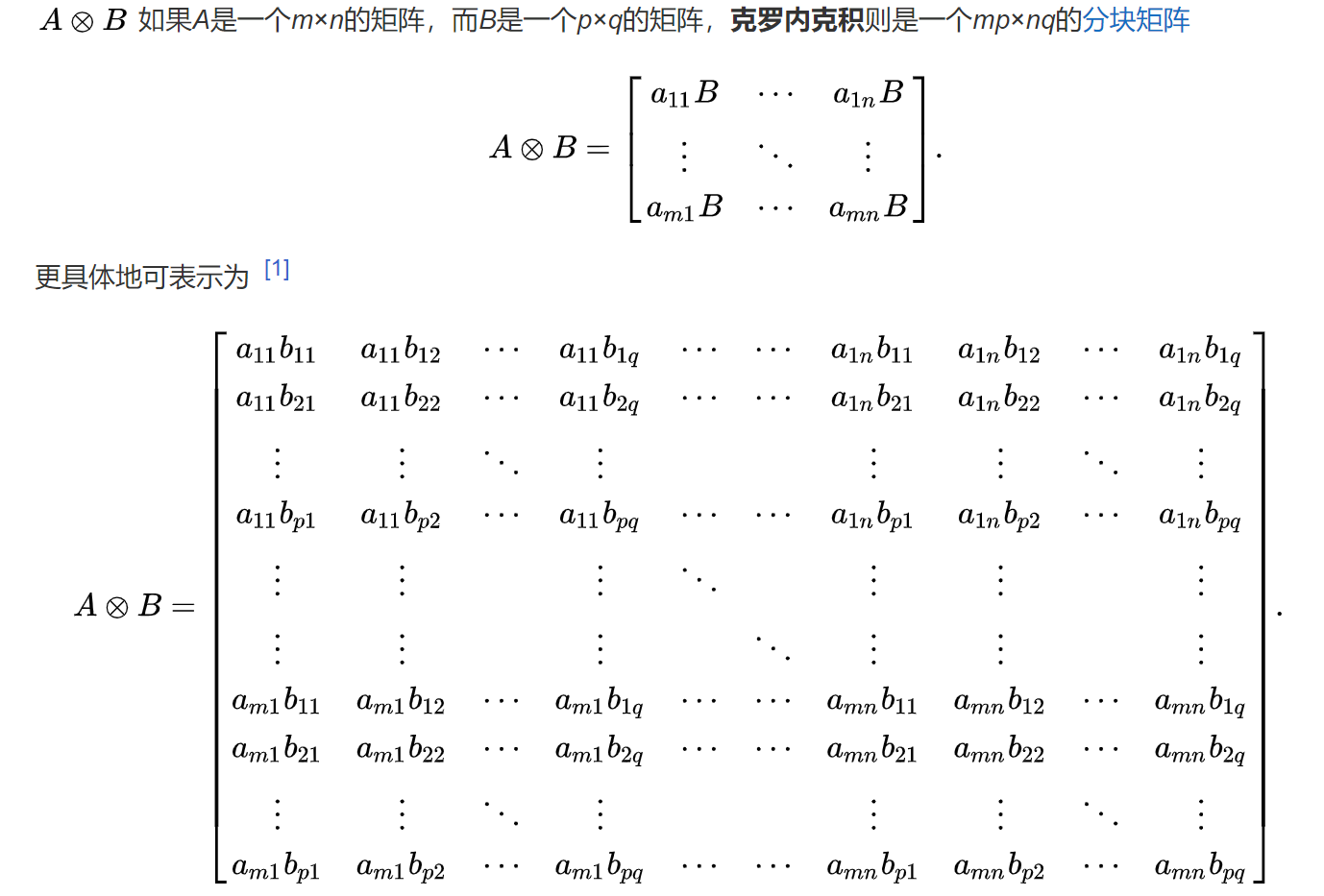
所以我的理解是 卷积仍然是普通的卷积，但是卷积核发生了变化，卷积核的变化过程中采用了克罗内克积。