Full卷积、Same卷积、Valid卷积、带深度的一维卷积

转载和参考以下几个链接：https://www.cnblogs.com/itmorn/p/11177439.html;

https://blog.csdn.net/jack__linux/article/details/91357456?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~aggregatepage~first_rank_v2~rank_aggregation-2-91357456.pc_agg_rank_aggregation&utm_term=same%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C&spm=1000.2123.3001.4430

一维卷积通常有三种类型：full卷积、same卷积和valid卷积，下面以一个长度为5的一维张量I和长度为3的一维张量K（卷积核）为例，介绍这三种卷积的计算过程

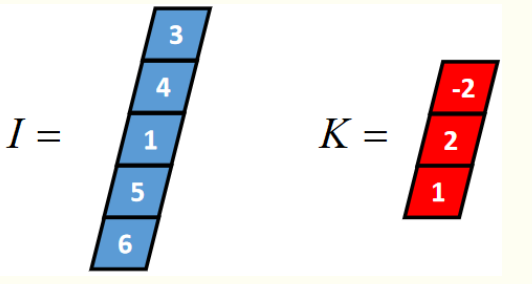
一维FULL卷积

Full卷积的计算过程是：K沿着I顺序移动，每移动到一个固定位置，对应位置的值相乘再求和，计算过程如下：

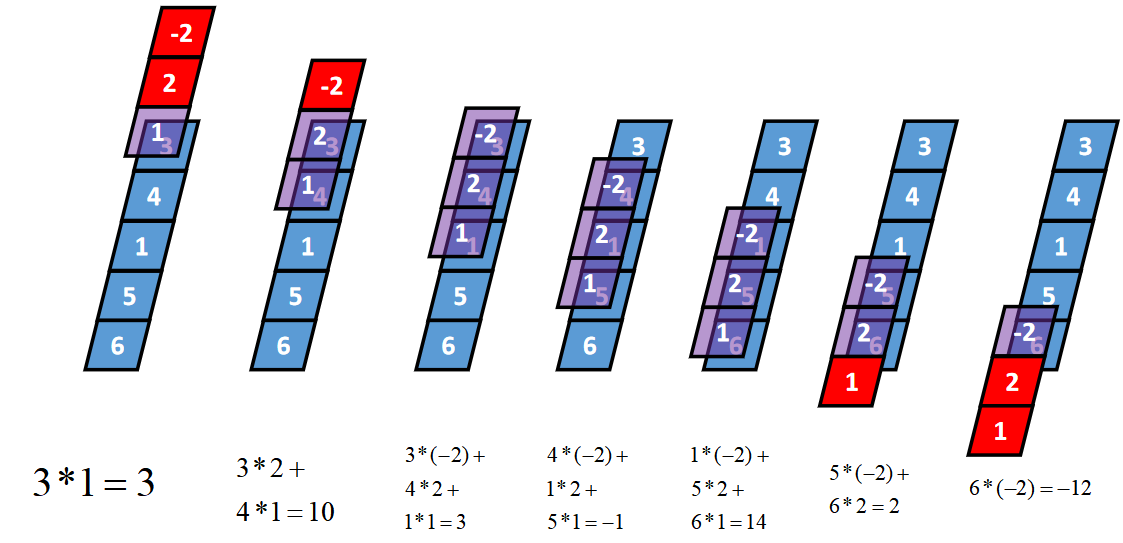
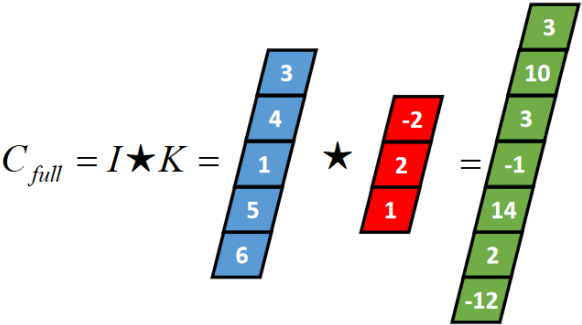
将得到的值依次存入一维张量C_full，该张量就是I和卷积核K的full卷积结果，其中K卷积核或者滤波器或者卷积掩码，卷积符号用符号★表示，记C_full=I★K

一维Same卷积

卷积核K都有一个锚点，然后将锚点顺序移动到张量I的每一个位置处，对应位置相乘再求和，计算过程如下：

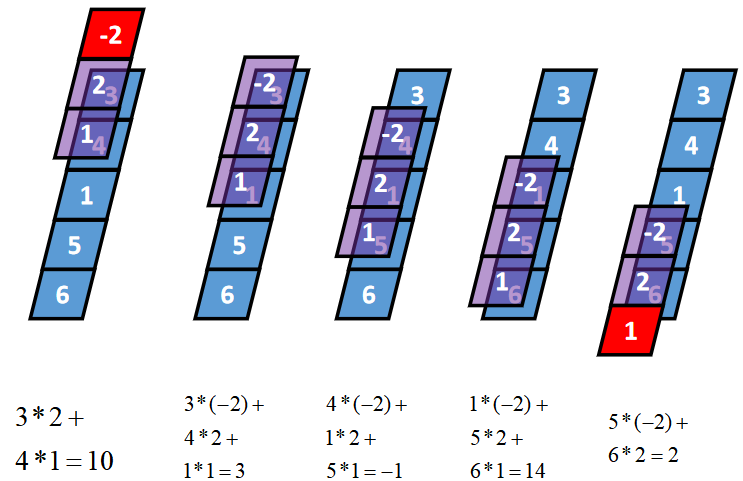
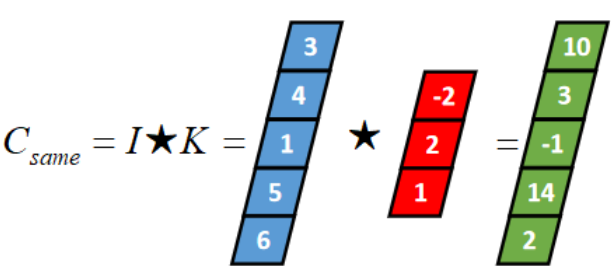
假设卷积核的长度为FL，如果FL为奇数，锚点位置在(FL-1)/2处；如果FL为偶数，锚点位置在(FL-2)/2处。

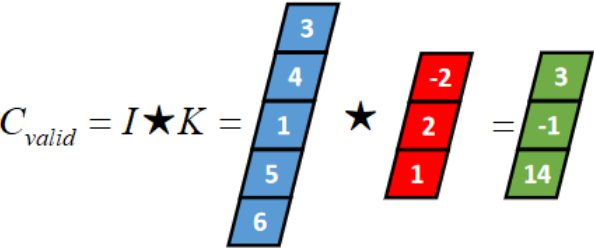
一维Valid卷积  

从full卷积的计算过程可知，如果K靠近I，就会有部分延伸到I之外，valid卷积只考虑I能完全覆盖K的情况，即K在I的内部移动的情况，计算过程如下：

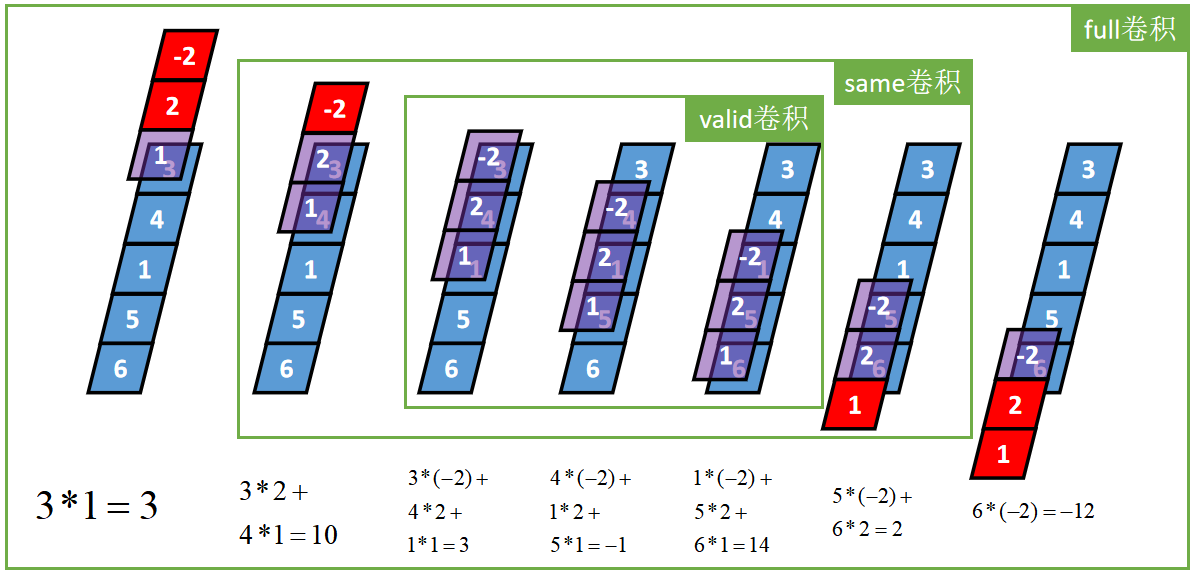
三种卷积类型的关系

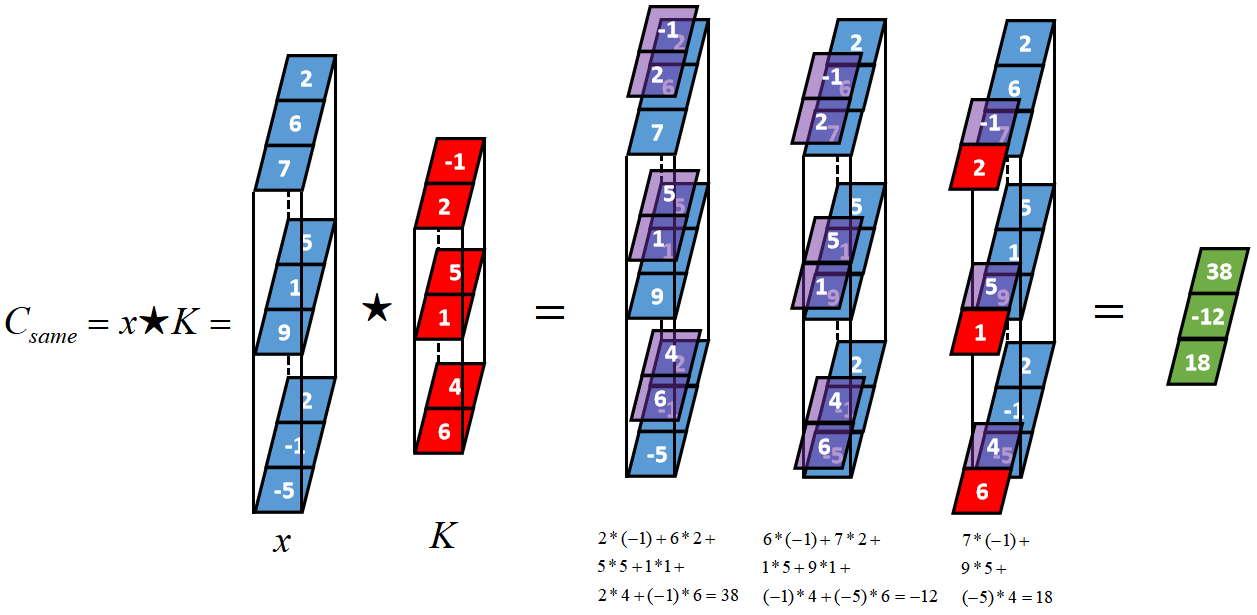
具备深度的一维卷积

比如x是一个长度为3，深度为3的张量，其same卷积过程如下，卷积核K的锚点在张量x范围内依次移动，输入张量的深度和卷积核的深度是相等的。

具备深度的张量与多个卷积核的卷积

上面介绍了一个张量和一个卷积核进行卷积。他们的深度相等才能进行卷积，下面介绍一个张量与多个卷积核的卷积。同一个张量与多个卷积核的卷积本质上是该张量分别与每一个卷积核卷积，然后将每一个卷积结果在深度方向上连接起来。

举例：以长度为3、深度为3的输入张量与2个长度为2、深度为3的卷积核卷积为例，过程如下：

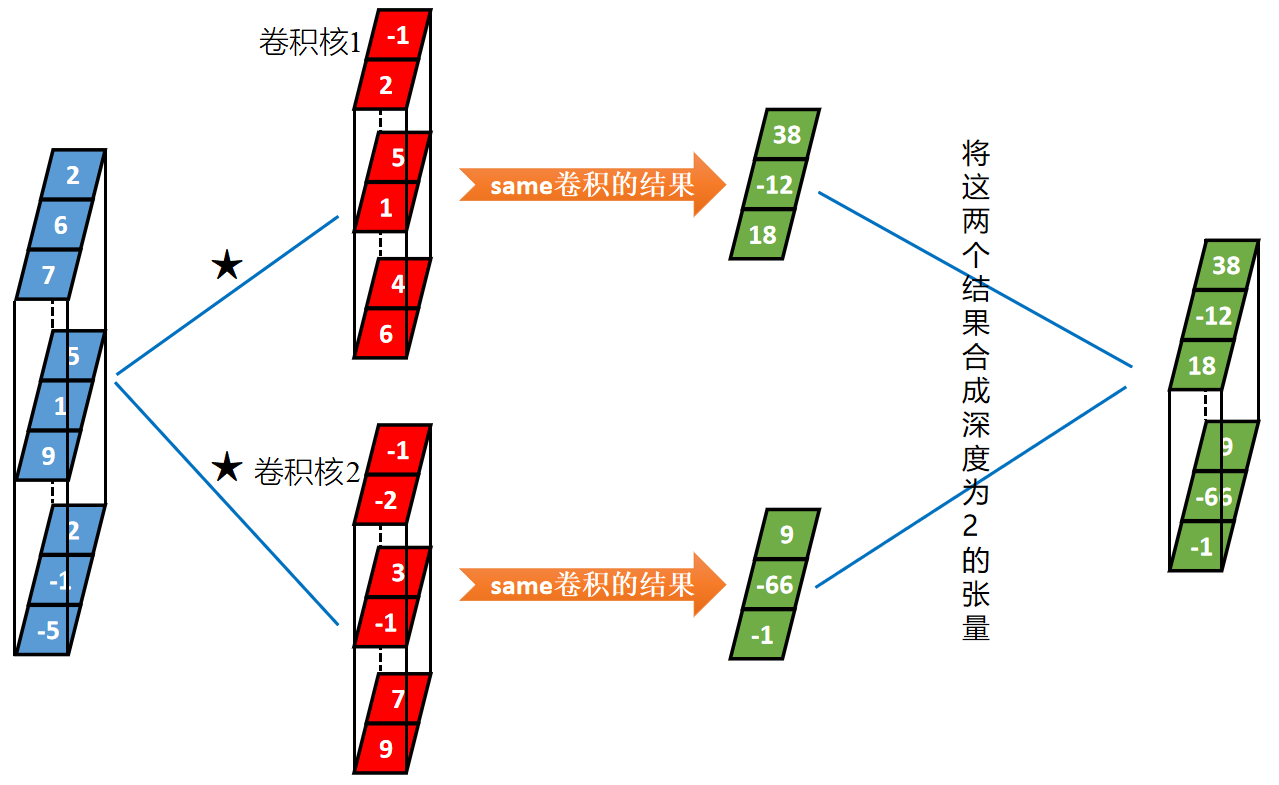
参考资料

《图解深度学习与神经网络：从张量到TensorFlow实现》_张平

 一下参考：https://blog.csdn.net/leviopku/article/details/80327478

本文清晰展示三种模式的不同之处，其实这三种不同模式是对卷积核移动范围的不同限制。

设 image的大小是7x7，filter的大小是3x3

1，full mode

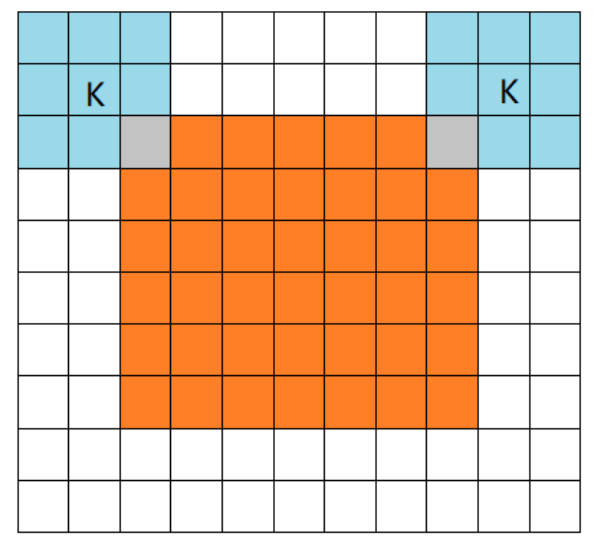
橙色部分为image, 蓝色部分为filter。full模式的意思是，从filter和image刚相交开始做卷积，白色部分为填0。filter的运动范围如图所示。

2，same mode

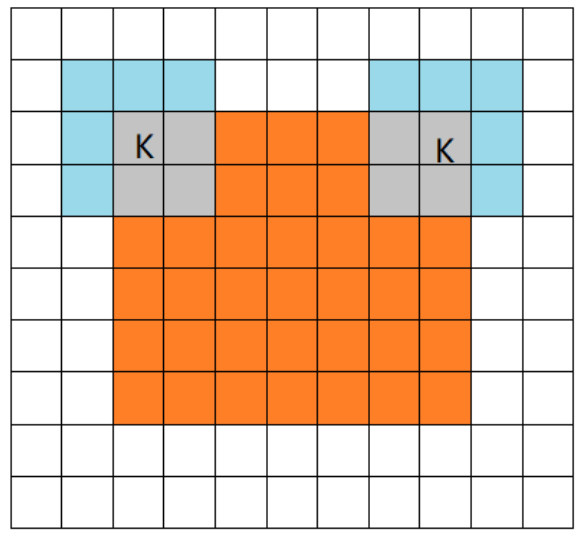
当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)。

3.valid

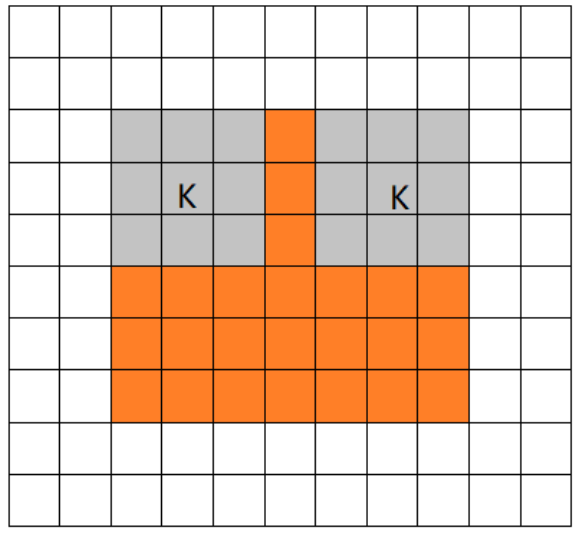
当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

lenet-5可以参考这个链接讲解，链接内有讲的不太好，甚至不太对的地方，注意甄别：

https://max.book118.com/html/2016/1215/72627902.shtm

同时参考：深度学习与目标检测 第三章部分。杜鹏等编著。isbn：9787121367854