[CSP day1T3]树上的数

题面

题解

这道题由于是求字典序最小的，所以要贪心地枚举数字，然后找可以走到的编号最小的点，处理这条路径。

这条路径有一些特性。

以下是特别精炼的结论：

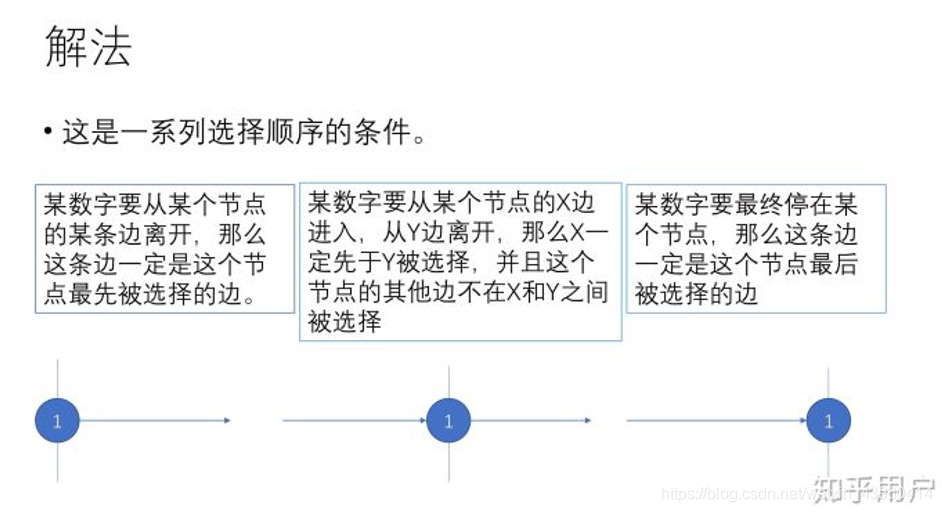
所以一旦选好了路径，这些边的先后顺序就被定死了，后面的路径肯定不能与他冲突

于是我们只要记录边的先后关系，然后进行非常严密的逻辑判断选择一条不冲突的路径。

复杂度O(n^2)

Code

你们看不懂的

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<stack>
#include<algorithm>
#define LL long long
using namespace std;
int read() {
	int f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
	return x * f;
}
struct ed{
	int v,id;
	ed(){}
	ed(int V,int I){v = V;id = I;}
};
vector<ed> g[2005];
int id[2005];
int pre[8005],suf[8005];
int fa[8005];
int le[8005];
int minn;
int find(int x) {
	if(fa[x] != x) fa[x] = find(fa[x]);
	return fa[x];
}
void unionSet(int a,int b) {
	int u = find(a),v = find(b);
	if(u < v) le[u] += le[v],fa[v] = u;
	else le[v] += le[u],fa[u] = v;
}
int n,m,i,j,s,o,k;
void dfs(int x,int fat,int fai) {
	if(fai != 0 && (((find(fai) > n || le[find(fai)] == g[x].size()) && !suf[fai] && !pre[x + n]) || g[x].size() == 1)) minn = min(minn,x);
//	printf("minn:%d x:%d find[%d]:%d\n",minn,x,fai,find(fai));
	for(int i = 0;i < g[x].size();i ++) {
		int y = g[x][i].v,z = g[x][i].id;
		if((fai == 0 && (((find(z) > 2*n || le[find(z)] == g[x].size()) && !pre[z] && !suf[x]) || g[x].size() == 1)) || (y != fat && !pre[z] && !suf[fai] && find(fai) != find(z) && !(find(fai) <= n && find(z) <= 2*n && le[find(fai)] + le[find(z)] != g[x].size()))) {
			int zi = z;
			if(zi <= 3 * n) zi += n;
			else zi -= n;
			dfs(g[x][i].v,x,zi);
		}
	}
	return ;
}
bool dfs2(int x,int fat,int mini,int fai) {
	if(x == mini) {
		suf[fai] = x + n;
		pre[x + n] = fai;
		unionSet(x + n,fai);
		return 1;
	}
	bool ff = 0;
	for(int i = 0;i < g[x].size();i ++) {
		if(g[x][i].v != fat) {
			int z = g[x][i].id,zi = g[x][i].id;
			if(z <= 3*n) z += n;
			else z -= n;
			bool fff = ff;
			ff |= dfs2(g[x][i].v,x,mini,z);
			if(!fff && ff) {
				if(fai == 0) {
					pre[zi] = x;
					suf[x] = zi;
					unionSet(x,zi);
				}
				else {
					pre[zi] = fai;
					suf[fai] = zi;
					unionSet(fai,zi);
				}
			}
		}
	}
	return ff;
}
int main() {
//	freopen("tree.in","r",stdin);
//	freopen("tree.out","w",stdout);
	int T;
	scanf("%d",&T);
	while(T --) {
		scanf("%d",&n);
		memset(pre,0,sizeof(pre));
		memset(suf,0,sizeof(suf));
		memset(le,0,sizeof(le));
		for(int i = 1;i < n;i ++) {
			id[i] = read();
			g[i].clear();
			fa[i] = i;
			fa[i + n] = i + n;
			fa[i + 2*n] = i + n*2;
			fa[i + 3*n] = i + n*3;
		}
		scanf("%d",&id[n]);
		g[n].clear();
		fa[n] = n;
		fa[2*n] = 2*n;
		fa[3*n] = 3*n;
		fa[4*n] = 4*n;
		for(int i = 1;i < n;i ++) {
			s = read();o = read();
			g[s].push_back(ed(o,i + n*2));
			g[o].push_back(ed(s,i + n*3));
			le[i + n*2] = le[i + n * 3] = 1;
		}
//		for(int i = 1;i <= n;i ++) printf("p:%d size:%d\n",i,g[i].size());
		for(int i = 1;i <= n;i ++) {
			s = id[i];
			minn = 0x7f7f7f7f;
//			cout<<"point:"<<i<<"("<<s<<")"<<endl;
			dfs(s,0,0);
			if(minn <= n) {
				id[i] = minn;
				dfs2(s,0,minn,0);
			}
		}
		for(int i = 1;i <= n;i ++) {
			printf("%d ",id[i]);
		}putchar('\n');
	}
	return 0;
}