LeetCode 周赛 341 场，模拟 / 树上差分 / Tarjan 离线 LCA / DFS

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 提问。

大家好，我是小彭。

上周末有单双周赛，双周赛我们讲过了，单周赛那天早上有事没参加，后面做了虚拟竞赛，然后整个人就不好了。前 3 题非常简单，但第 4 题有点东西啊，差点就放弃了。最后，被折磨了一个下午和一个大夜总算把第 4 题做出来了，除了新学的 Tarjon 离线算法，这道题还涉及到树上差分、前缀和、DFS、图论等基础知识，几度被折磨得想要放弃。这种感觉，似乎和当年在 LeetCode 上做前 10 题的时候差不多哈哈。

加油吧，没有什么经验是随随便便能够获得的，默默努力，愿君共勉。

---

周赛大纲

2643. 一最多的行（Easy）

简单模拟题，无需解释。

• 模拟：$O(nm)$

2644. 找出可整除性得分最大的整数（Easy）

简单模拟题，和 Q1 几乎相同，这场周赛出的不好。

• 模拟：$O(nm)$

2645. 构造有效字符串的最少插入数（Medium）

中等模拟题，不难。

• 模拟：$O(n)$

2646. 最小化旅行的价格总和（Hard）

这道题的考点非常多，难度也非常高。先掌握暴力 DFS 的解法，再分析暴力解法中重复计算的环节，最后推出树上差分和离线 Tarjan 算法。这道题非常非常复杂，

• 递归中递和归的思想，再理解一下：为什么你学不会递归？谈谈我的经验
• 并查集问题，不要错过：如何使用并查集解决朋友圈问题？
• 差分数组问题，这个点还没有写，同系列的前缀和数组可以参考：使用前缀和数组解决 “区间和查询” 问题
• 题解 1：暴力 DFS $O(nm)$
• 题解 2：树上差分 + Tarjan 离线 LCA + DFS $O(n + \alpha m)$

---

2643. 一最多的行（Easy）

题目地址

https://leetcode.cn/problems/row-with-maximum-ones/

题目描述

给你一个大小为 m x n 的二进制矩阵 mat ，请你找出包含最多 1 的行的下标（从 0 开始）以及这一行中 1 的数目。

如果有多行包含最多的 1 ，只需要选择 行下标最小 的那一行。

返回一个由行下标和该行中 1 的数量组成的数组。

题解（模拟）

简单模拟题。

class Solution {
    fun rowAndMaximumOnes(mat: Array<IntArray>): IntArray {
        var maxIndex = 0
        var maxCount = 0
        for (i in 0 until mat.size) {
            var count = 0
            for (j in 0 until mat[0].size) {
                count += mat[i][j]
            }
            if (count > maxCount) {
                maxCount = count
                maxIndex = i
            }
        }
        return intArrayOf(maxIndex, maxCount)
    }
}

复杂度分析：

• 时间复杂度：$O(nm)$
• 空间复杂度：$O(1)$

---

2644. 找出可整除性得分最大的整数（Easy）

题目地址

https://leetcode.cn/problems/find-the-maximum-divisibility-score/

题目描述

给你两个下标从 0 开始的整数数组 nums 和 divisors 。

divisors[i] 的 可整除性得分 等于满足 nums[j] 能被 divisors[i] 整除的下标 j 的数量。

返回 可整除性得分 最大的整数 divisors[i] 。如果有多个整数具有最大得分，则返回数值最小的一个。

题解（模拟）

简单模拟题。

class Solution {
    fun maxDivScore(nums: IntArray, divisors: IntArray): Int {
        var maxDivisor = 0
        var maxCount = -1
        for (divisor in divisors) {
            var count = 0
            for (num in nums) {
                if (num % divisor == 0) count++
            }
            if (count > maxCount || count == maxCount && divisor < maxDivisor) {
                maxDivisor = divisor
                maxCount = count
            }
        }
        return maxDivisor
    }
}

复杂度分析：

• 时间复杂度：$O(nm)$
• 空间复杂度：$O(1)$

---

2645. 构造有效字符串的最少插入数（Medium）

题目地址

https://leetcode.cn/problems/minimum-additions-to-make-valid-string/

题目描述

给你一个字符串 word ，你可以向其中任何位置插入 "a"、"b" 或 "c" 任意次，返回使 word 有效 需要插入的最少字母数。

如果字符串可以由 "abc" 串联多次得到，则认为该字符串 有效 。

题解（模拟）

维护当前状态与目标状态，当两个状态存在偏差时，插入偏差的字符数。

class Solution {
    fun addMinimum(word: String): Int {
        val n = word.length
        var targetStatus = 0
        var index = 0
        var ret = 0
        while (index < n) {
            // 当前状态
            val curStatus = word[index] - 'a'
            // 插入
            ret += (curStatus + 3 - targetStatus) % 3
            // 目标状态
            targetStatus = (curStatus + 1) % 3
            index++
        }
        ret += when (targetStatus) {
            0 -> 0
            1 -> 2
            2 -> 1
            else -> 0
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

---

2646. 最小化旅行的价格总和（Hard）

题目地址

https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/

题目描述

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

问题分析

分析 1：题目的数据结构是树而不是图，所以节点之间的最短路是唯一的，不需要使用最短路算法。从节点 start 到节点 end 的最优路径是 start 到最近公共祖先（LCA）+ 最近公共祖先（LCA）到 end；

分析 2：题目可以选择将一些节点的价格减半，显然价格越高的节点越应该减半，或者访问次数越多的节点越应该减半。所以我们可以先对每个 trips[i] 跑一次 DFS，并统计每个节点的访问次数 cnts[i]，将每个节点的价格更新为 prices[i] * cnts[i]

分析 3：类似于 337. 打家劫舍 III，如果我们选择将节点 x 减半（偷窃），那么与 x 相邻的节点便不能减半（偷窃）：

• 如果 prices[x] 减半，那么 x 的最近子节点不能减半；
• 如果 prices[x] 不变，那么 x 的最近子节点可以减半，也可以不减半，选择两种情况的更优解。

题解一（暴力 DFS）

根据问题分析，我们的算法是：

• 1、先枚举每种旅途，统计每个节点的访问次数（总共跑 m 次 DFS）；
• 2、更新每个节点的价格权重为 prices[i] * cnts[i]；
• 3、任意选择一个节点为根节点跑一次 DFS，在每一层递归中通过子问题的解得出原问题的解，每个子问题的解有「减半」和「不减半」两种结果；
• 4、最终，根据根节点的问题求出最终解。

class Solution {
    fun minimumTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        // 建树
        val graph = Array(n) { LinkedList<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0])
        }
        // 统计节点访问次数
        val cnts = IntArray(n)
        for (trip in trips) {
            cntDfs(graph, cnts, trip[0], trip[1], -1)
        }
        // 更新价格
        for (i in 0 until n) {
            price[i] *= cnts[i]
        }
        // DFS（打家劫舍）
        val ret = priceDfs(graph, price, 0, -1)
        return Math.min(ret[0], ret[1])
    }

    // return：是否找到目标节点
    private fun cntDfs(graph: Array<LinkedList<Int>>, cnts: IntArray, cur: Int, target: Int, parent: Int): Boolean {
        // 终止条件（目标节点）
        if (cur == target) {
            cnts[cur]++
            return true
        }
        // 枚举子节点（树的特性：每个方向最多只会访问一次，不需要使用 visit 数组）
        for (to in graph[cur]) {
            // 避免回环
            if (to == parent) continue
            // 未找到
            if (!cntDfs(graph, cnts, to, target, cur)) continue
            // 找到目标路径，不需要再检查其他方向
            cnts[cur]++
            return true
        }
        return false
    }

    // return：以 cur 为根节点的子树的最大价格 <cur 不变, cur 减半>
    private fun priceDfs(graph: Array<LinkedList<Int>>, price: IntArray, cur: Int, parent: Int): IntArray {
        val ret = intArrayOf(
            price[cur],     // x 不变
            price[cur] / 2 // x 减半
        )
        // 枚举子节点（树的特性：每个方向最多只会访问一次，不需要使用 visit 数组）
        for (to in graph[cur]) {
            // 避免回环
            if (to == parent) continue
            // 子树结果
            val childRet = priceDfs(graph, price, to, cur)
            ret[0] += Math.min(childRet[0], childRet[1])
            ret[1] += childRet[0]
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(nm)$ 其中 m 为 trips 数组的长度，每轮 DFS 的时间是 $O(n)$，计数时间为 $O(nm)$，打家劫舍 DFS 的时间为 $O(n)$；
• 空间复杂度：$O(n + m)$ 树空间 + DFS 递归栈空间，递归深度最大为 n。

题解一的瓶颈在于 cntDfs 中的 m 次 DFS 搜索，如何优化？

预备知识：差分数组

在 cntDfs 中的每一次 DFS 搜索中，我们需要将 [start, end] 路径上的节点访问次数 +1，这正好类似于在数组上将 [start, end] 区间的位置 + 1，符合 “差分数组” 的应用场景。我们可以在树上做差分，再通过一次 DFS 搜索中计算节点的访问次数。

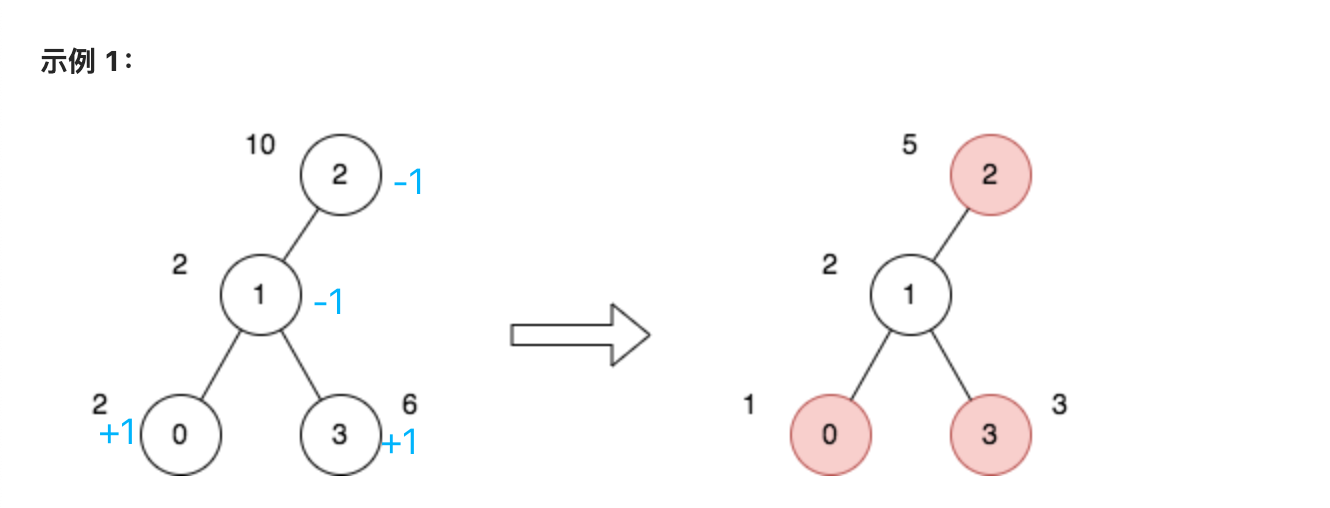
例如在示例 1 中，我们的路径是 (0, 3)，那么路径相当于 [0] + [1,3]，针对这两条路径的差分为：

• [0]：diff[0]++，diff[father[0]] —，即 diff[1] —
• [1, 3]：diff[3]++，diff[father[1]] —，即 diff[2]—

那怎么计算访问次数呢？跟差分数组一样，对差分数组计算前缀和就可以获得节点的访问次数，我们在归的过程中累加差分值，例如 节点 1 的访问次数就是 +1 + 1 - 1 等于 1 次。

题解二（树上差分 + Tarjan 离线 LCA + DFS）

考虑到旅行路径列表是固定的，我们可以使用 Tarjan 离线算法，预先求出所有旅行路径端点的最近公共祖先。反之，如果旅行路径列表是动态的， 那么离线算法就力不从心了，需要使用复杂度更高的在线算法。

参考资料：

• LCA最近公共祖先（Tarjan离线算法）
• 图论 · LCA 最近公共祖先

在题解一中，我们需要花费 m 次 DFS 搜索来解决 m 个 LCA 问题，Tarjan 算法的核心思路是在一次 DFS 搜索的过程中解决所有 LCA 查询问题：

• 1、任选一个点为根节点，从根节点开始。
• 2、「递」的过程（分解子问题）：遍历该点 u 所有子节点 v，并标记这些子节点 v 已被访问过，若是 v 还有子节点，返回 2 继续「递」；
• 3、「归」的过程：寻找与 u 有查询关系的点 k。如果 k 节点已经被访问过，那么 u 和 k 的最近公共祖先就是当前 u 和 k 所在的分组根节点；
• 4、节点 u 的问题结束后，将 节点 u 合并到父节点的集合上。

细节说明：Tarjan 算法递的过程是寻找查询关系，当路径的两个端点都访问过，那么这两个端点必然处在同一个分组中，而它们的分组根节点正好就是最近公共组件；

细节说明：为什么分组根节点正好就是最近公共组件？因为归是按照 DFS 的搜索顺序回归的；

细节说明：如何合并 v 到 u 的集合上？这是并查集的操作，我们定义 parent[x] 表示 x 节点的所处的分组，初始状态 parent[x] = x；

细节说明：如何查询与 u 有查询关系的点 k？预处理准备映射表；

细节说明：为了区分阶段状态，我们定义 color[x] 表示节点 x 的状态，0 表示未访问、1 表示处于递归栈中，2 表示结束。

更多细节，看代码吧。

class Solution {
    fun minimumTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        // 建树
        val graph = Array(n) { LinkedList<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0])
        }
        // 查询关系
        val search = Array(n) { LinkedList<Int>() }
        for (trip in trips) {
            search[trip[0]].add(trip[1])
            // 当路径两端相同时，避免重复
            if (trip[0] != trip[1]) search[trip[1]].add(trip[0])
        }
        val unionFind = UnionFind(n, graph, search)
        unionFind.tarjan(0, -1/* 无父节点 */)

        // DFS（打家劫舍）
        val ret = priceDfs(graph, price, unionFind.diff, 0, -1)
        return Math.min(ret[0], ret[1])
    }

    // 并查集
    private class UnionFind(val n: Int, val graph: Array<LinkedList<Int>>, val search: Array<LinkedList<Int>>) {
        // 并查集数据结构
        private val parent = IntArray(n) { it }

        // 树上的父节点
        private val father = IntArray(n)

        // Tarjan 状态
        private val colors = IntArray(n) //  表示未访问、1 表示处于递归栈中，2 表示结束

        // 树上差分
        val diff = IntArray(n)

        private fun find(x: Int): Int {
            // 路径压缩
            if (x != parent[x]) parent[x] = find(parent[x])
            return parent[x]
        }

        // 这道题的合并不能使用按秩合并，必须将子节点 x 合并到 y 的集合中
        private fun merge(x: Int, y: Int) {
            // 按秩合并
            val rootX = find(x)
            val rootY = find(y)
            if (rootX != rootY) parent[rootX] = rootY
        }

        fun tarjan(u: Int, fa: Int) {
            // 记录父节点
            father[u] = fa
            // 标记已访问
            colors[u] = 1
            // 递的过程：遍历 u 的所有子节点 v
            for (v in graph[u]) {
                if (0 != colors[v]) continue // 访问过
                // 继续递的过程
                tarjan(v, u)
            }
            // 枚举查询关系
            for (k in search[u]) {
                if (k == u || colors[k] == 2) {
                    // 找到 u 和 k 的查询关系，更新树上差分
                    val lca = find(k)
                    diff[u]++
                    diff[lca]--
                    diff[k]++
                    val lcaParent = father[lca]
                    if (lcaParent >= 0) diff[lcaParent]--
                }
            }
            // 结束
            colors[u] = 2
            if(fa != -1) merge(u, fa) // 将子节点 u 合并到 fa 的集合中
        }
    }

    // return：以 cur 为根节点的子树的最大价格 <cur 不变, cur 减半>
    private fun priceDfs(graph: Array<LinkedList<Int>>, price: IntArray, diff: IntArray, cur: Int, parent: Int): IntArray {
        val ret = intArrayOf(0, 0, diff[cur])
        // 枚举子节点（树的特性：每个方向最多只会访问一次，不需要使用 visit 数组）
        for (to in graph[cur]) {
            // 避免回环
            if (to == parent) continue
            // 子树结果
            val childRet = priceDfs(graph, price, diff, to, cur)
            ret[0] += Math.min(childRet[0], childRet[1])
            ret[1] += childRet[0]
            ret[2] += childRet[2] // 累加前缀和
        }
        ret[0] += price[cur] * ret[2]
        ret[1] += price[cur] * ret[2] / 2
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n + \alpha m)$ 其中 m 为 trips 数组的长度，$\alpha$ 是并查集的反阿克曼函数，近似于线性函数；
• 空间复杂度：$O(n + m)$ 树空间 + DFS 递归栈空间，递归深度最大为 n。

---