DP：LCS（最长公共子串、最长公共子序列）

1. 两者区别

约定：在本文中用 LCStr 表示最长公共子串（Longest Common Substring），LCSeq 表示最长公共子序列（Longest Common Subsequence）。

子串要求在原字符串中是连续的，而子序列则没有要求。例如：

字符串 s1=abcde，s2=ade，则 LCStr=de，LCSeq=ade。

2. 求最长公共子串（LCStr）

算法描述：构建如下图的矩阵dp[][]，当s1[i] == s2[j] 的时候，dp[i][j]=1；最后矩阵中斜对角线上最长的“1”序列的长度，就是 LCStr 的长度。

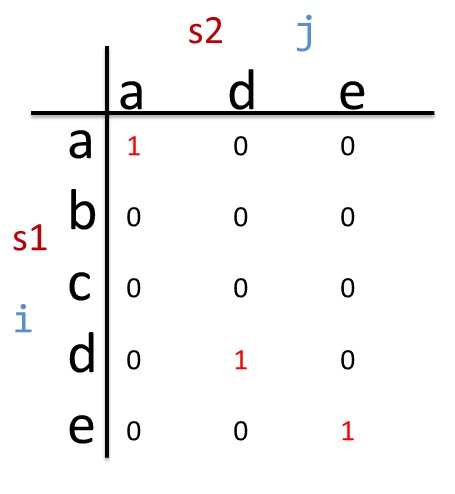
但是求矩阵里斜线上的最长的“1”序列，仍然略显麻烦，我们进行如下优化：当要往矩阵中填“1”的时候，我们不直接填“1”，而是填“1”+左上角的那个数。如下图所示：

这样，我们只需求出矩阵里的最大数（注意：最大数可不一定在最右下角，别误解了上图），即是 LCStr 的长度。

要求出这个 LCStr，其他的不多说了，见代码中注释。

C++ code：

 #include <iostream>
 #include <string>
 #include <cstdlib>         // freopen
 #include <cstring>         // memset
 using namespace std;

 #define MAXN 2001
 static int dp[MAXN][MAXN];

 string LCStr(const string &s1, const string &s2)
 {
     string result;

     //s1纵向，s2横向
     //len1行，len2列
     int len1=s1.length(), len2=s2.length();
     memset(dp,,sizeof(dp));

     //预先处理第一行第一列
     for(int i=; i<len2; ++i)
         if(s1[]==s2[i]) dp[][i]=;
     for(int i=; i<len1; ++i)
         if(s1[i]==s2[]) dp[i][]=;

     for(int i=; i<len1; ++i)
     for(int j=; j<len2; ++j)
         if(s1[i]==s2[j]) dp[i][j]=dp[i-][j-]+;    //矩阵填充 

     //将第一行的最大值移到最右边
     for(int i=; i<len2; ++i)
         if(dp[][i]<dp[][i-]) dp[][i]=dp[][i-];

     //从第二行开始，将每一行的最大值移到最右边
     //最后边的数和上一行的最右边数比较大小，将大的下移
     //到最后，右下角的数就是整个矩阵的最大值
     for(int i=; i<len1; ++i)
     {
         for(int j=; j<len2; ++j)
             if(dp[i][j]<dp[i][j-]) dp[i][j]=dp[i][j-];
         if(dp[i][len2-]<dp[i-][len2-]) dp[i][len2-]=dp[i-][len2-];
     }
     cout<<"length of LCStr: "<<dp[len1-][len2-]<<endl;

     int max = dp[len1-][len2-];
     int pos_x;
     for(int i=; i<len1; ++i)
     for(int j=; j<len2; ++j)
     {
         if(dp[i][j]==max)
         {
             pos_x=i;
             j=len2;    ///
             i=len1;    ///快速跳出循环
         }
     }
     result=s1.substr(pos_x-max+,max);
     return result;
 }

 int main()
 {
     int t;
     freopen("in.txt","r",stdin);
     cin>>t;
     cout<<"total tests: "<<t<<endl<<endl;
     while(t--)
     {
         string a,b;
         cin>>a>>b;
         cout<<a<<endl<<b<<endl;

         string res=LCStr(a,b);
         cout<<"LCStr: "<<res<<endl<<endl;
     }
     return ;
 }

运行：

输入：

5
abcde
ade
flymouseEnglishpoor
comeonflymouseinenglish
BCXCADFESBABCACA
ABCACADF
programming
contest
123454567811267234678392
1457890567809713265738

输出：

3. 最长公共子序列（LCSeq）

算法描述：

矩阵最后的 dp[i][j] 就是 LCSeq 的长度。

为了把 LCSeq 求出来，我们在给每一个 dp[i][j] 赋值的时候，需要记住这个值来自于哪里。是来自于左上角（LEFTUP），还是上边（UP），还是左边（LEFT）。然后从矩阵最后一个元素回溯，就能找出 LCSeq。如下图：

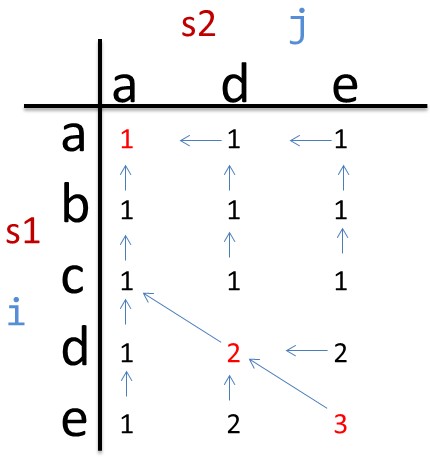
当 dp[i-1][j]==dp[i][j-1]，即左边的元素等于上边的元素时，我取上边的元素。（取左边的也行，并不影响程序结果。但在整个代码中要统一规则）。

C++ code：

 #include <iostream>
 #include <string>
 #include <cstring>        //memset
 #include <algorithm>    //reverse
 #define LEFTUP     0
 #define UP        1
 #define LEFT    2
 #define MAXN 2001
 using namespace std;

 //s1纵向，s2横向
 int dp[MAXN][MAXN];
 short path[MAXN][MAXN];
 string LCSeq(const string &s1, const string &s2)
 {
     int len1=s1.length(), len2=s2.length();
     string result="";

     //将dp[][]和path[][]的首行首列清零
     for(int j=; j<=len2; ++j)
         {dp[][j]=; path[][j]=;}
     for(int i=; i<=len1; ++i)
         {dp[i][]=; path[i][]=;}
     //以上代码用 memset 也行
     //memset(dp,0,sizeof(dp));
     //memset(path,0,sizeof(path));

     for(int i=; i<=len1; ++i)
     {
         for(int j=; j<=len2; ++j)
         {
             if(s1[i-]==s2[j-])
             {
                 dp[i][j]=dp[i-][j-]+;
                 path[i][j]=LEFTUP;
             }
             else if(dp[i-][j]>dp[i][j-])    //up>=left 这里是用 > 还是 >= ，当LCS不唯一时，对结果有影响，但长度一样
             {
                 dp[i][j]=dp[i-][j];
                 path[i][j]=UP;
             }
             else
             {
                 dp[i][j]=dp[i][j-];
                 path[i][j]=LEFT;
             }
         }
     } //矩阵填充完成
     cout<<"length of LCSeq: "<<dp[len1][len2]<<endl;

     int i=len1, j=len2;
     while(i> && j>)
     {
         if(path[i][j]==LEFTUP)
         {
             result+=s1[i-];
             i--;
             j--;
         }
         else if(path[i][j]==UP) i--;
         else if(path[i][j]==LEFT) j--;
     }
     reverse(result.begin(), result.end());
     return result;
 }

 int main()
 {
     int t;
     freopen("in.txt", "r", stdin);
     //freopen("out.txt", "w", stdout);
     cin>>t;
     cout<<"total tests: "<<t<<endl<<endl;
     while(t--)
     {
         string s1,s2;
         cin>>s1>>s2;
         cout<<s1<<endl<<s2<<endl;

         string res=LCSeq(s1,s2);
         cout<<"LCSeq: "<<res<<endl<<endl;

     }
     return ;
 }        

运行：

输入：同上

输出：

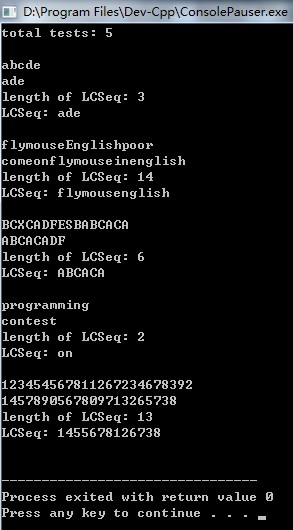
说一下以上程序中37行的 >= 和 > 的区别。当 LCSeq 不唯一时，讨论此区别才有意义。对于以下两个字符串

s1=BCXCADFESBABCACA  ， s2=ABCACADF

取>=和>符号时的求得的LCSeq分别为：

BCCADF 和 ABCACA

【s1=BCXCADFESBABCACA  ， s2=ABCACADF】

【s1=BCXCADFESBABCACA  ， s2=ABCACADF】

分析：

当取>=符号时，就是说当dp[i][j]上边的数与左边的数相等时，选择上边的数赋给dp[i][j]。这就造成在后来的回溯过程中，回溯的路径“更快地往上走，更慢的往左走”，当回溯结束时，所求的的子序列由“s2的靠后部分 + s1的靠前部分”构成。（这里的“靠前”、“靠后”为相对而言）。

当取>符号时，就是说当dp[i][j]上边的数与左边的数相等时，选择左边的数赋给dp[i][j]。这就造成在后来的回溯过程中，回溯的路径“更快地往左走，更慢的往上走”，当回溯结束时，所求的的子序列由“s1的靠后部分 + s2的靠前部分”构成。

可以参看上面的图来理解这个过程，也可自己画两个图试一下。

参考：

维基百科

http://en.wikipedia.org/wiki/Longest_common_substring_problem

http://en.wikipedia.org/wiki/Longest_common_subsequence_problem

http://en.wikibooks.org/wiki/Algorithm_implementation/Strings/Longest_common_substring

博客园

http://www.cnblogs.com/xudong-bupt/archive/2013/03/15/2959039.html

推荐：

http://blog.sina.com.cn/s/blog_54ce19050100wdvn.html

http://www.cnblogs.com/huangxincheng/archive/2012/11/11/2764625.html

http://my.oschina.net/leejun2005/blog/117167

http://www.cnblogs.com/zhangchaoyang/articles/2012070.html