hdu 5279 Reflect phi 欧拉函数

Reflect

Time Limit: 1 Sec

Memory Limit: 256 MB

题目连接

http://bestcoder.hdu.edu.cn/contests/contest_chineseproblem.php?cid=628&pid=1003

Description

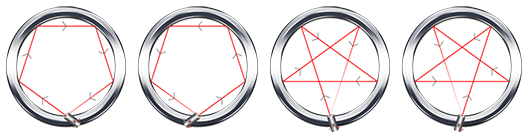
从镜面材质的圆上一点发出一道光线反射NN次后首次回到起点。
问本质不同的发射的方案数。

Input

第一行一个整数T，表示数据组数。T \leq 20T≤20
对于每一个组，第一行一个整数n(1 \leq n \leq 100)n(1≤n≤100)，接下来第二行nn个数允许前导零的非负整数A_iA​i​​，表示数列。保证A_iA​i​​位数\leq 100≤100。

Output

对于每一个组，输出共一行，包含一个整数，表示答案。

Sample Input

1 4

Sample Output

4

HINT

 

题意

题解：

暴力打表就好了

然后发现是欧拉函数phi

然后猜了一发结论交了一发

AC了

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
typedef long long LL;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 2000001
#define mod 10007
#define eps 1e-9
const int inf=0x7fffffff;   //无限大
/*

*/
//**************************************************************************************
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
LL phi[maxn],n;
void phi1()
{
    memset(phi,,sizeof(phi));
    phi[]=;
    for(LL i=;i<=n;i++)
    {
        if(!phi[i])
        {
            for(LL j=i;j<=n;j+=i)
            {
                if(!phi[j]) phi[j]=j;
                phi[j]=phi[j]/i*(i-);
            }
        }
    }
}
int main()
{
    int t=read();
    n=;
    phi1();
    while(t--)
    {
        int x=read();
        cout<<phi[x+]<<endl;
    }
}