Codeforces 460D. Little Victor and Set

D. Little Victor and Set

time limit per test：1 second

memory limit per test：256 megabytes

input：standard input

output：standard output

Little Victor adores the sets theory. Let us remind you that a set is a group of numbers where all numbers are pairwise distinct. Today Victor wants to find a set of integers S that has the following properties:

• for all x 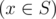 the following inequality holds l ≤ x ≤ r;
• 1 ≤ |S| ≤ k;
• lets denote the i-th element of the set S as si; value 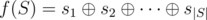 must be as small as possible.

Help Victor find the described set.

Input

The first line contains three space-separated integers l, r, k (1 ≤ l ≤ r ≤ 1012; 1 ≤ k ≤ min(106, r - l + 1)).

Output

Print the minimum possible value of f(S). Then print the cardinality of set |S|. Then print the elements of the set in any order.

If there are multiple optimal sets, you can print any of them.

Examples

input

8 15 3

output

1
2
10 11

input

8 30 7

output

0
5
14 9 28 11 16

Note

Operation 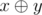 represents the operation of bitwise exclusive OR. In other words, it is the XOR operation.

分析：

分类讨论：

No.1 r-l<=10

直接暴力搜索...

No.2 k=1

此时直接输出l...

No.3 k=2

ans一定是1...(相邻两个xor一下...)

No.4 k>=4

ans一定是0...(相邻4个xor一下...)

No.5 k=3

我们找出最小的m使得2^m大于l...

这样，如果存在三个数x=2^m-1,y=2^m+2^(m-1),z=2^m+2^(m-1)-1，那么就一定可以是0，否则若y>r，ans一定是1...

证明如下：

如果存在m+1能够满足解，那么m也一定可以找到合法解...

因为要使得ans=0，所以第m位一定存在两个1，因此m-1位一定存在1，所以最大值的下界是2^m+2^(m-1)-1，最小值的上界是2^m-1...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
#define int long long
using namespace std;
//眉眼如初，岁月如故 

int l,r,k,ans,vis;

inline void dfs(int x,int tmp,int lala,int cnt){
    if(lala)
        if(ans>=tmp)
            ans=tmp,vis=lala;
    if(x==r+1||cnt>k)
        return;
    dfs(x+1,tmp,lala,cnt);dfs(x+1,tmp^x,lala|(1<<x-l),cnt+1);
}

signed main(void){
    scanf("%I64d%I64d%I64d",&l,&r,&k);
    if(r-l<=10){
        ans=r;dfs(l,0,0,1);printf("%I64d\n",ans);ans=vis;int cnt=0;
        while(ans)
            cnt+=ans&1,ans>>=1;
        printf("%I64d\n",cnt);cnt=0;
        while(vis){
            if(vis&1)
                printf("%I64d ",l+cnt);
            cnt++,vis>>=1;
        }
        puts("");
    }
    else if(k==1)
        printf("%I64d\n1\n%I64d\n",l,l);
    else if(k==2){
        puts("1");puts("2");
        if(l&1)
            printf("%I64d %I64d",l+1,l+2);
        else
            printf("%I64d %I64d",l,l+1);
    }
    else if(k>=4){
        puts("0");puts("4");
        if(l&1){
            for(int i=l+1;i<=l+4;i++)
                printf("%I64d ",i);
            puts("");
        }
        else{
            for(int i=l;i<=l+3;i++)
                printf("%I64d ",i);
            puts("");
        }
    }
    else{
        int m,L=1,R=62;
        while(L<=R){
        	int mid=(L+R)>>1;
        	if((1LL
			<<mid)>l)
        		m=mid,R=mid-1;
        	else
        		L=mid+1;
        }
        if(m==0){
        	puts("1");puts("2");
	            if(l&1)
	                printf("%I64d %I64d",l+1,l+2);
	            else
	                printf("%I64d %I64d",l,l+1);
        }
        else{
	        if((1LL<<m)+(1LL<<m-1)>r){
	            puts("1");puts("2");
	            if(l&1)
	                printf("%I64d %I64d",l+1,l+2);
	            else
	                printf("%I64d %I64d",l,l+1);
	        }
	        else{
	            puts("0");puts("3");int x=(1LL<<m)-1,y=(1LL<<m)+(1LL<<m-1),z=(1LL<<m)+(1LL<<m-1)-1;
	            printf("%I64d %I64d %I64d\n",x,y,z);
	        }
    	}
    }
    return 0;
}//Cap ou pas cap. Pas cap.

　　

---

By NeighThorn