hdu6311（ 2018 Multi-University Training Contest 2）

bryce1010模板

http://acm.hdu.edu.cn/showproblem.php?pid=6311

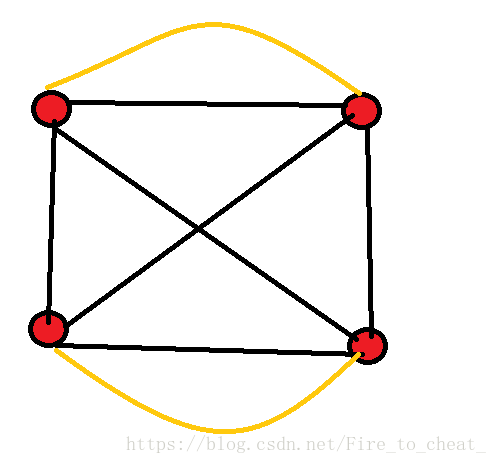
从dls思路中，我整理一下自己的思路：

1、首先也是建图

2、建图结束后，一个dfs查找联通块和度数为奇数的点

从第二对奇数度点开始给奇数度点对开始加辅助边（>2*m+1）

3. 加辅助边后，一个dfs搜索所有的奇数度顶点，如果碰到一个虚边，则res+2；

最后一笔画的个数为max(res/2,1)

/*hdu6311cover
题意：给出一张无向图，问多少次一笔画能覆盖整张图。
dls的思路：
1.对给出的数据建图
2.搜索图中的联通块和度为奇数的点
3.在联通块内的奇数对额外添加虚边(添加奇数点个数/2条边)
4.dfs得到最后结果

一张联通图n笔画完，则n=max(|degree(奇数)|/2,1)
每次添加一条边，则度数+2
当图上至多只有一对奇数度的点时，便可以一笔走过所有的边
删除额外添加的边（序号为>2*m+1）得到结果
*/

#include<bits/stdc++.h>
using namespace std;

const int MAXN=1e5+10;
struct Edge
{
    int to,next;//to保存终点，next保存邻接的边
    bool able;
}edge[MAXN<<2];

int n,m;
int Degree[MAXN];//每个点的度
int Head[MAXN];//每个点的最后一条边加入的边的序号
int cnt;//边的序号
int res;//一共找到的路径

bool vis[MAXN];
vector<int>st;//保存一个连通块中度为奇数的点
vector<int>road[MAXN];

void add(int u,int v)
{
    edge[++cnt].next=Head[u];
    edge[cnt].to=v;
    edge[cnt].able=true;
    Head[u]=cnt;
    ++Degree[u];
}
void add_edge(int u,int v)
{
    add(u,v);
    add(v,u);
}

//找到联通块和奇数点的度
 void dfs(int s)
 {
     vis[s]=true;
     if(Degree[s]&1)st.push_back(s);
     for(int i=Head[i];i;i=edge[i].next)
     {
         if(!vis[edge[i].to])dfs(edge[i].to);
     }
 }

void dfs2(int s)
{
    for(int i=Head[s];i;i=edge[i].next)
    {
        if(edge[i].able)
        {
            edge[i].able=edge[i^1].able=false;
            dfs2(edge[i].to);
            if(i>2*m+1)++res;//说明此边是由奇数度添加得到的，所以这条回路结束
            else
            {
                road[res].push_back(i/2*(2*(i&1)-1));
            }
        }
    }
}

int main()
{
    int u,v;
    while(cin>>n>>m)
    {
        cnt=1;res=0;
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            add_edge(u,v);
        }
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&Degree[i])
            {
                dfs(i);//找到联通块和奇数度的点
                if(st.empty())
                {
                    st.push_back(i);
                    st.push_back(i);
                }
                for(int j=2;j<st.size();j+=2)
                {//从第二对开始的奇数度的点添加一条双向边
                    add_edge(st[j],st[j+1]);
                }
                res++;
                dfs2(st[0]);
                st.clear();
            }
        }
        printf("%d\n",res);
        for(int i=1;i<=res;i++)
        {
            printf("%d",road[i].size());
            for(int j=0;j<road[i].size();j++)
            {
                printf(" %d",road[i][j]);
            }
            puts("");
            road[i].clear();
        }
        for(int i=1;i<=n;i++)
        {
            vis[i]=false;
            Head[i]=0;
            Degree[i]=0;
        }

        return 0;

    }

}