BZOJ2326 [HNOI2011]数学作业 【矩阵快速幂】

题解##

我们设f[i]表示前i个数模M意义下的答案

则f[i] = f[i - 1] * 100...0 + i【i是几位就有几个0】

可以写出矩阵递推式：

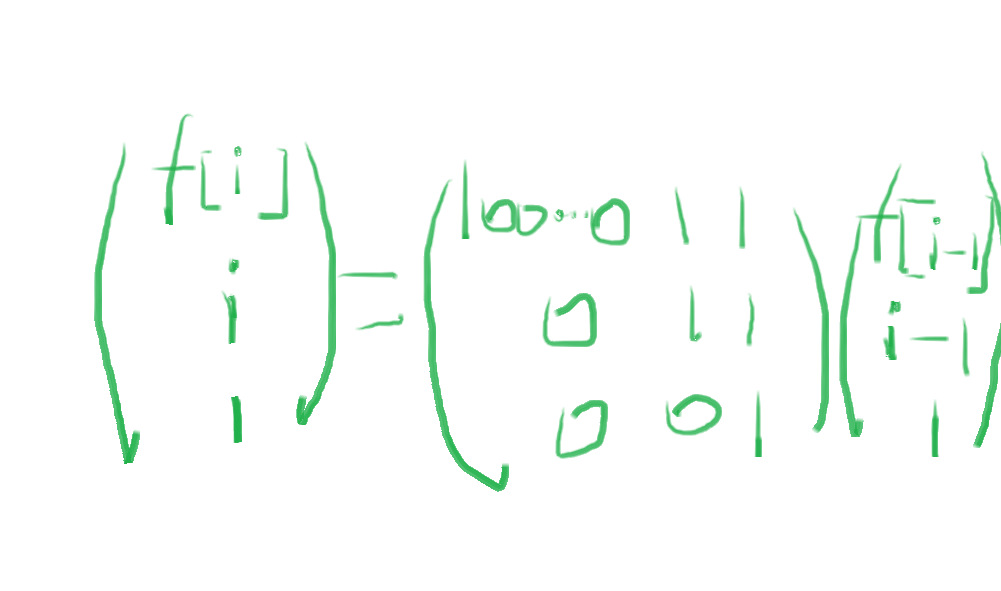
之后按位数分组矩乘就好了

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define cls(s) memset(s,0,sizeof(s))
using namespace std;
const int maxn = 100005,maxm = 100005,INF = 1000000000;
LL N,M;
struct Matrix{
	LL s[3][3],n,m;
	Matrix(){cls(s); n = m = 0;}
}A,F;
Matrix operator *(const Matrix& a,const Matrix& b){
	Matrix ans;
	if (a.m !=b.n) return ans;
	ans.n = a.n; ans.m = b.m;
	for (int i = 0; i < ans.n; i++)
		for (int j = 0; j < ans.m; j++)
			for (int k = 0; k < a.m; k++)
				ans.s[i][j] = (ans.s[i][j] + a.s[i][k] * b.s[k][j] % M) % M;
	return ans;
}
Matrix qpow(Matrix a,LL b){
	Matrix ans; ans.n = ans.m = a.n;
	for (int i = 0; i < ans.n; i++) ans.s[i][i] = 1;
	for (; b; b >>= 1,a = a * a)
		if (b & 1) ans = ans * a;
	return ans;
}
int S[][3] = {
	{1,1,1},
	{0,1,1},
	{0,0,1}
};
int main(){
	cin >> N >> M;
	A.n = A.m = 3;
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			A.s[i][j] = S[i][j];
	F.n = 3; F.m = 1;
	F.s[0][0] = 0; F.s[1][0] = 0; F.s[2][0] = 1;
	for (LL bit = 1; ; bit *= 10){
		A.s[0][0] = bit % M * 10 % M;
		if (N < bit * 10){
			F = qpow(A,N - bit + 1) * F;
			break;
		}else F = qpow(A,bit * 10 - bit) * F;
	}
	cout << F.s[0][0] << endl;
	return 0;
}