算法学习记录-查找——二叉排序树（Binary Sort Tree）

二叉排序树 也称为 二叉查找数。

它具有以下性质：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

它的左、右子树也分别为二叉排序树。

　　之前的查找折半查找、斐波那契查找、插值查找的前提条件就是序列为有序，为顺序存储结构。我们在查找一章提过，查找还有动态查找，比如插入和删除操作，

进行这些操作对顺序存储结构效率不那么高。能不能有一种既静态查找效率高，动态查找效率也高呢？

　　联想之前的堆排序，人们创造出一个堆这样的结构来提高排序效率。（佩服他们的思维）堆结构建立在二叉树上，之前一直都不知道二叉树是怎么用的，

看到这里二叉树的作用就体现出来了，我们定义二叉排序树来实现动、静态查找效率都高的结构。

　　先举一个例子：

先看看一个无序序列排列好的二叉排序树：

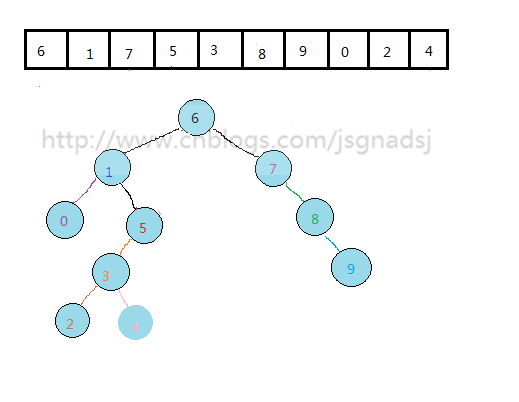
上图中，上面数组是原始数组，下面的二叉排序树是按照上面的原始数组来构建的。

1.我们如果按中序遍历得到的结果就是这个序列的 顺序排序结果。｛0，1，2，3，4，5，6，7，8，9｝

2.我们实现静态查找，查找关键字8：

　　从根结点开始，根结点（6），8比6大，往右（到结点（7））。

　　当前结点（7）,8比该结点大，往右（到结点（8））。

　　找到8。

这里有点类似折半、斐波那契、插值查找的思想。所以它的静态查找效率比较高。

　

3.动态查找（插入和删除）

如果要插入记录10到这个序列中，我们只需要给它找一个合适的位置，在对插入后的二叉树中序遍历的时候，依旧是一个顺序排列表。

　　插入10，比根结点（6）大，向右（到结点7）

　　比当前结点（7）大，向右（到结点8）

　　比当前结点（8）大，向右（到结点9）

　　比当前结点（9）大，向右，无孩子，则建立孩子并赋值10.

　　完成后，该树的中序遍历依然是一个顺序表，对原先树几乎是没有影响，所以其插入操作也非常的高效。

对于其删除：

由于二叉排序树在删除一个记录时候要保证其中序遍历的顺序不受影响，操作要分几种情况，会稍微麻烦点，这个后面再讲。

所以综合看来，这样的二叉排序树对 静动态操作 基本都高效，避免了有序表的插入删除时候的大量记录的移动。

---

到这里，看到了二叉排序数的好处，

问题就来了!

怎么从一个无序的数列构建这样的二叉排序树？

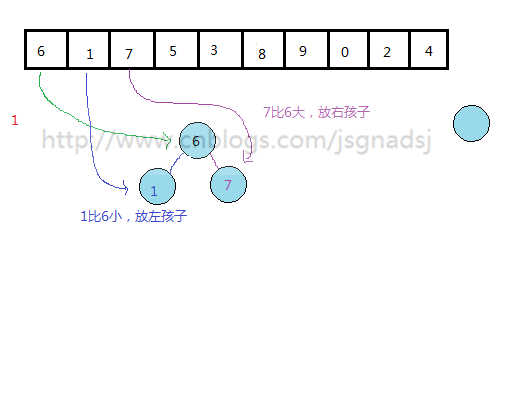
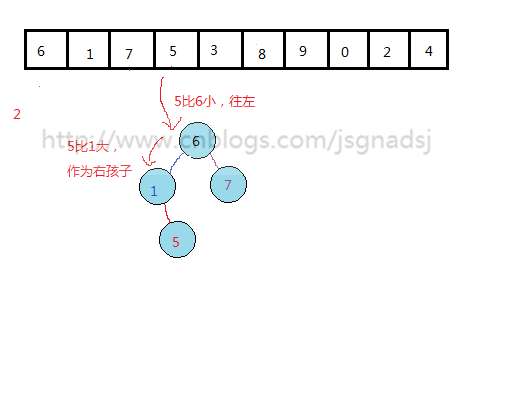
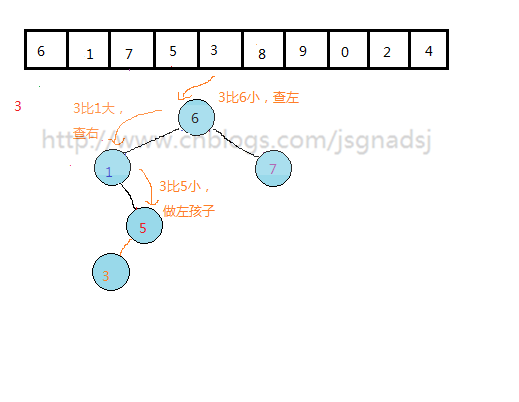
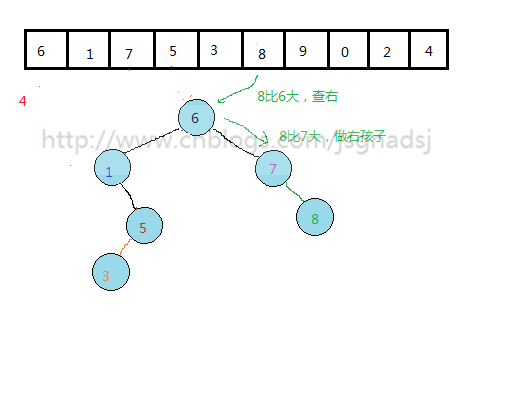
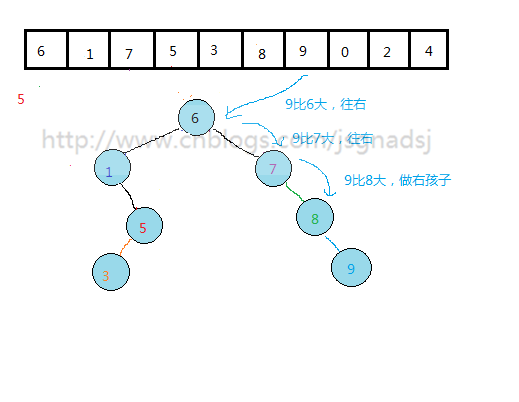
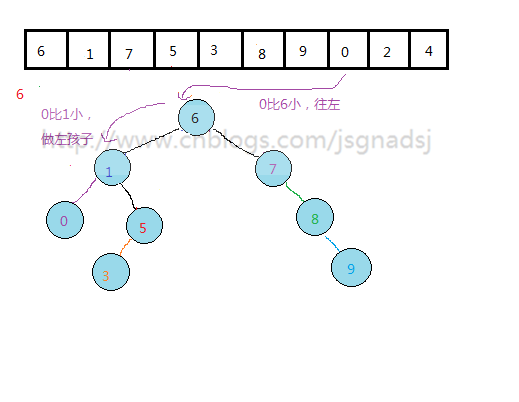
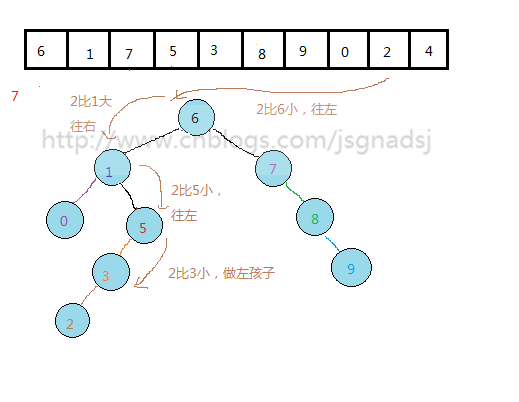
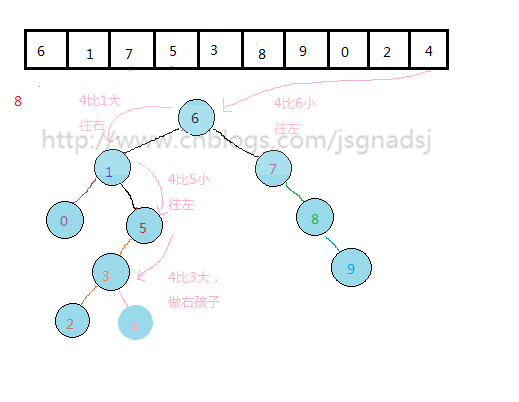
通过上面过程，基本能够看出无序表到二叉排序树的构建过程。

其实质就是查找与插入操作。先查看结点是否存在，然后比较，再插入。

知道了思想，写程序就不难了。

插入算法程序如下：

 bool SearchBST(pBinNode T,myDataType key,pBinNode *pNode)//pNode是指针，需要修改，所以用二级指针,该指针用来记录要查找结点，若不存在则返回将插入结点的父结点。
 {                //根结点指针，寻找的值，记录父节点值
     if (T == NULL)//如果是空树，则父结点指向NULL
     {
         *pNode = NULL;
         return false;
     }
     pBinNode crntNode = T;

     while(crntNode)//找到要插入结点的父结点
     {
         if (crntNode->data == key)
         {
             return true;
         }
         else if(crntNode->data > key)
         {
             *pNode = crntNode;
             crntNode = crntNode->lchd;
         }
         else if (crntNode->data < key)
         {
             *pNode = crntNode;
             crntNode = crntNode->rchd;
         }
     }
     return false;
 }

 bool insertBSTNode(pBinNode *T,int key,int index)//第一个参数之所以为二级指针，因为在该函数中有malloc生成的是指针，而要将该指针的值在函数中赋给另一个指针，所以要用指针的指针才能接收
 {
     pBinNode n=NULL;
     pBinNode p=NULL;
     if (false == SearchBST(*T,key,&p))//找到要插入的结点的父结点p
     {
         n = (pBinNode)malloc(sizeof(BinNode));
         if (n == NULL)
         {
             printf("error:no more memery!\n");
             return false;
         }
         (*n).data = key;
         (*n).index = index;
         (*n).lchd = NULL;
         (*n).rchd = NULL;

         if (p == NULL)
         {
             *T = n;
         }
         else if(key < p->data)
         {
             p->lchd = n;
         }
         else if (key > p->data)
         {
             p->rchd = n;
         }
         return true;
     }
     else
     {
         return false;
     }
 }

仔细想想这样的Search是不是可以用递归的调用方法。

删除操作，对于删除有三种情况：

1. 欲删除的结点是叶子结点，由于删除不破坏树结构，只需要修改其父结点指向为NULL，然后free该欲删除的结点。
2. 欲删除的结点只有左子树或者只有右子树，只需要将欲删除的结点的父结点孩子指针指向其（左/右）子树，然后free欲删除的结点。
3. 欲删除的结点既有左子树又有右子树，此时不能如上面两种方法处理。

　　　　最简单的方法就是将他的左右子树重新排序，按二叉排序树条件组成新的子树，再连接到树上。这样做会非常的复杂，假如删除的是根结点，那么意味着整个树将要重新构成。

　　　　我们想想二叉排序树的中序遍历，其中序遍历就是无序序列的有序集合。

　　　　我们删除其中一个结点，通过调整方法，尽可能减少破坏树的结构，我们只要在调整后，如果能保证调整后的树的中序遍历依然是有序集合，那么这样的调整就能成功。

举几个例子：

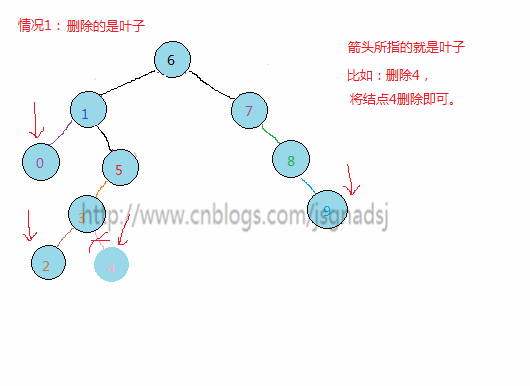
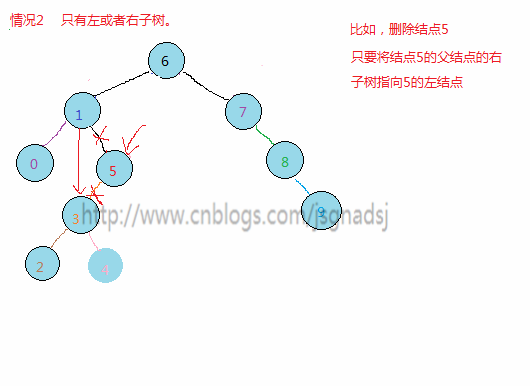
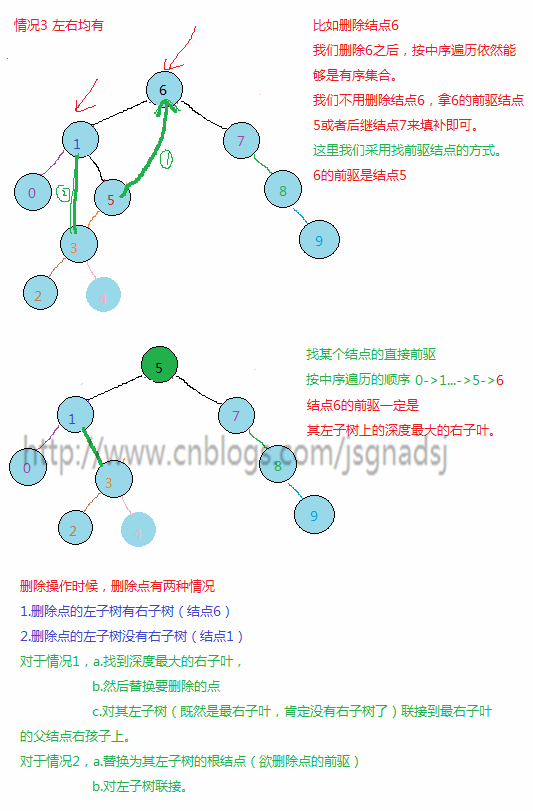
代码：

 void DeleteNode(pBinNode *fNode,pBinNode *sNode)//参数分别为 父亲 和 孩子
 {
     pBinNode q = NULL;
     pBinNode s = NULL;
     if ((*sNode)->rchd == NULL)//右子树为空，只要把它的左子树直接连上就行
     {
         q = *sNode;
         (*fNode)->rchd = (*sNode)->lchd;
         free(q);
     }
     else if((*sNode)->lchd == NULL)//左子树为空，只要把它的右子树直接连上就可以了。
     {
         q=*sNode;
         (*fNode)->rchd = (*sNode)->rchd;
         free(q);
     }
     else //左右都不为空！
     {
         q = *sNode;
         s = (*sNode)->lchd;//其前驱一定是在左子树上的最后一个右分支
         while(s->rchd)
         {
             q = s;
             s=s->rchd;
         }
         (*sNode)->data = s->data;
         if (q != *sNode)
         {
             q->rchd = s->lchd;
         }
         else
         {
             q->lchd= s->lchd;
         }
         free(s);

     }
 }

 bool DeleteBST(pBinNode *T,int key)//找是否存在关键字
 {
     if (!(*T))
     {
         return false;
     }

     pBinNode s = *T;//son
     pBinNode f = NULL;//father

     while(s)
     {
         if(key == s->data)
         {
             //删除
             DeleteNode(&f,&s);
             return true;
         }
         else if (s->data > key)
         {
             f = s;
             s = s->lchd;
         }
         else if (s->data < key)
         {
             f = s;
             s = s->rchd;
         }
     }
     return false;//no value in array
 }

完整程序：

 #include <stdlib.h>

 typedef int myDataType;
 //myDataType src_ary[10] = {9,1,5,8,3,7,6,0,2,4};
 //myDataType src_ary[10] = {1,2,3,4,5,6,7,8,9,10};
 //myDataType src_ary[10] = {10,9,8,7,6,5,4,3,2,1};

 myDataType src_ary[] = {,,,,,,,,,};

 //****************树结构***********************//
 typedef struct BTS{
     myDataType data;
     int index;
     struct BTS *lchd,*rchd;
 }BinNode,*pBinNode;

 void prt_ary(myDataType *ary,int len)
 {
     int i=;
     while(i < len)
     {
         printf(" %d ",ary[i++]);
     }
     printf("\n");
 }

 bool SearchBST(pBinNode T,myDataType key,pBinNode *pNode)//pNode是指针，需要修改，所以用二级指针,该指针用来记录要查找结点，若不存在则返回将插入结点的父结点。
 {                //根结点指针，寻找的值，记录父节点值
     if (T == NULL)//如果是空树，则父结点指向NULL
     {
         *pNode = NULL;
         return false;
     }
     pBinNode crntNode = T;

     while(crntNode)//找到要插入结点的父结点
     {
         if (crntNode->data == key)
         {
             return true;
         }
         else if(crntNode->data > key)
         {
             *pNode = crntNode;
             crntNode = crntNode->lchd;
         }
         else if (crntNode->data < key)
         {
             *pNode = crntNode;
             crntNode = crntNode->rchd;
         }
     }
     return false;
 }

 bool insertBSTNode(pBinNode *T,int key,int index)//第一个参数之所以为二级指针，因为在该函数中有malloc生成的是指针，而要将该指针的值在函数中赋给另一个指针，所以要用指针的指针才能接收
 {
     pBinNode n=NULL;
     pBinNode p=NULL;
     if (false == SearchBST(*T,key,&p))//找到要插入的结点的父结点p
     {
         n = (pBinNode)malloc(sizeof(BinNode));
         if (n == NULL)
         {
             printf("error:no more memery!\n");
             return false;
         }
         (*n).data = key;
         (*n).index = index;
         (*n).lchd = NULL;
         (*n).rchd = NULL;

         if (p == NULL)
         {
             *T = n;
         }
         else if(key < p->data)
         {
             p->lchd = n;
         }
         else if (key > p->data)
         {
             p->rchd = n;
         }
         return true;
     }
     else
     {
         return false;
     }
 }

 void DeleteNode(pBinNode *fNode,pBinNode *sNode)//参数分别为 父亲 和 孩子
 {
     pBinNode q = NULL;
     pBinNode s = NULL;
     if ((*sNode)->rchd == NULL)//右子树为空，只要把它的左子树直接连上就行
     {
         q = *sNode;
         (*fNode)->rchd = (*sNode)->lchd;
         free(q);
     }
     else if((*sNode)->lchd == NULL)//左子树为空，只要把它的右子树直接连上就可以了。
     {
         q=*sNode;
         (*fNode)->rchd = (*sNode)->rchd;
         free(q);
     }
     else //左右都不为空！
     {
         q = *sNode;
         s = (*sNode)->lchd;//其前驱一定是在左子树上的最后一个右分支
         while(s->rchd)
         {
             q = s;
             s=s->rchd;
         }
         (*sNode)->data = s->data;
         if (q != *sNode)
         {
             q->rchd = s->lchd;
         }
         else
         {
             q->lchd= s->lchd;
         }
         free(s);

     }
 }

 bool DeleteBST(pBinNode *T,int key)//找是否存在关键字
 {
     if (!(*T))
     {
         return false;
     }

     pBinNode s = *T;//son
     pBinNode f = NULL;//father

     while(s)
     {
         if(key == s->data)
         {
             //删除
             DeleteNode(&f,&s);
             return true;
         }
         else if (s->data > key)
         {
             f = s;
             s = s->lchd;
         }
         else if (s->data < key)
         {
             f = s;
             s = s->rchd;
         }
     }
     return false;//no value in array
 }

 int _tmain(int argc, _TCHAR* argv[])
 {
     int i;
     pBinNode T=NULL;//排序树的根结点

     for (i=;i<;i++)//创建树
     {
         if (false == insertBSTNode(&T,src_ary[i],i))
         {
             printf("error:src_ary[%d]=%d\n",i,src_ary[i]);
         }
     }
     DeleteBST(&T,);//删除6
     //DeleteBST(&T,8);
     getchar();
     return ;
 }

测试结果：

在178出设置断点。

程序运行到178行之前，变量结果：

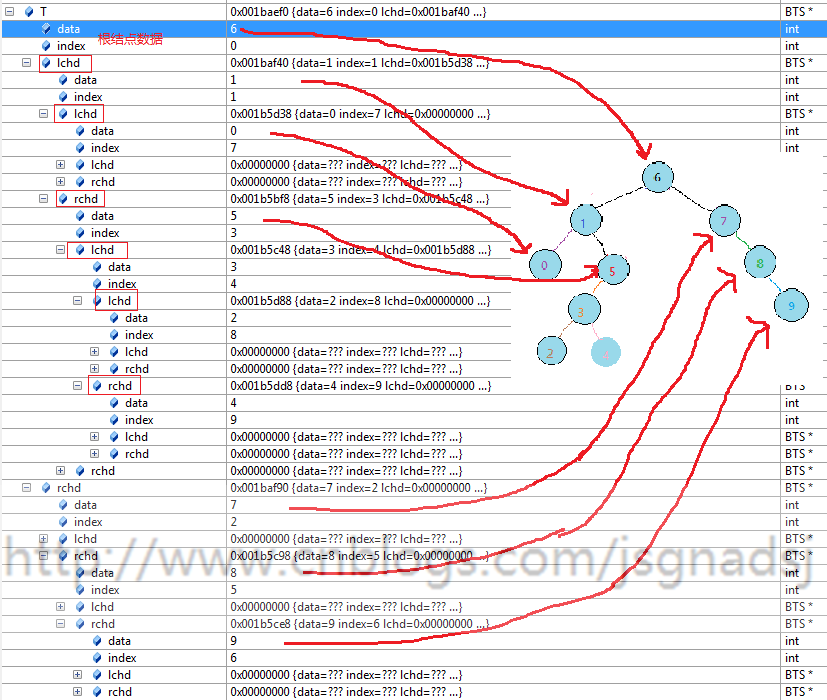
运行到179，执行了178行后

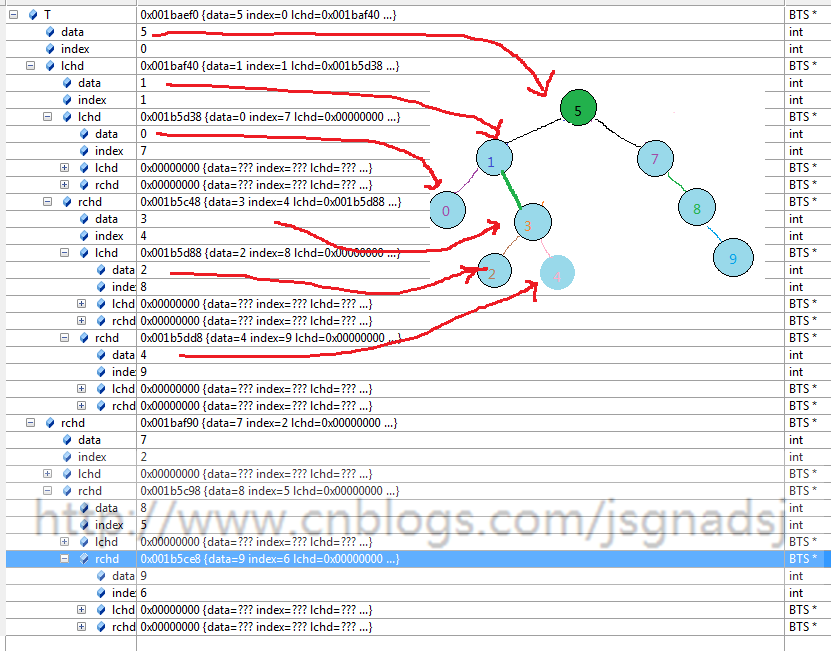
另外两种可以自己测试下。

补充，另外还有一种方法写程序，递归

 //********************************
 int DeleteNode_R(pBinNode *p)
 {
 //    printf("data=%d\n",(*p)->data);
 //    return 0;
     pBinNode q = NULL;
     pBinNode s = NULL;
     if ((*p)->rchd == NULL)//右子树为空，只要把它的左子树直接连上就行
     {
         q = *p;
         (*p) = (*p)->lchd;
         free(q);
     }
     else if((*p)->lchd == NULL)//左子树为空，只要把它的右子树直接连上就可以了。
     {
         q=*p;
         (*p) = (*p)->rchd;
         free(q);
     }
     else //左右都不为空！
     {
         q = *p;
         s = (*p)->lchd;//其前驱一定是在左子树上的最后一个右分支
         while(s->rchd)
         {
             q = s;
             s=s->rchd;
         }
         (*p)->data = s->data;
         if (q != *p)
         {
             q->rchd = s->lchd;
         }
         else
         {
             q->lchd= s->lchd;
         }
         free(s);
     }
     return ;
 }

 int DeleteBST_R(pBinNode *T,int key)
 {
     if (!(*T))
     {
         return false;
     }
     else
     {
         if ((*T)->data == key)
         {
             return DeleteNode_R(T);
         }
         else if(key > (*T)->data)
         {
             return DeleteBST_R(&(*T)->rchd,key);
         }
         else if (key < (*T)->data)
         {
             return DeleteBST_R(&(*T)->lchd,key);
         }
     }
 }