树剖 lca

GeneralLiu

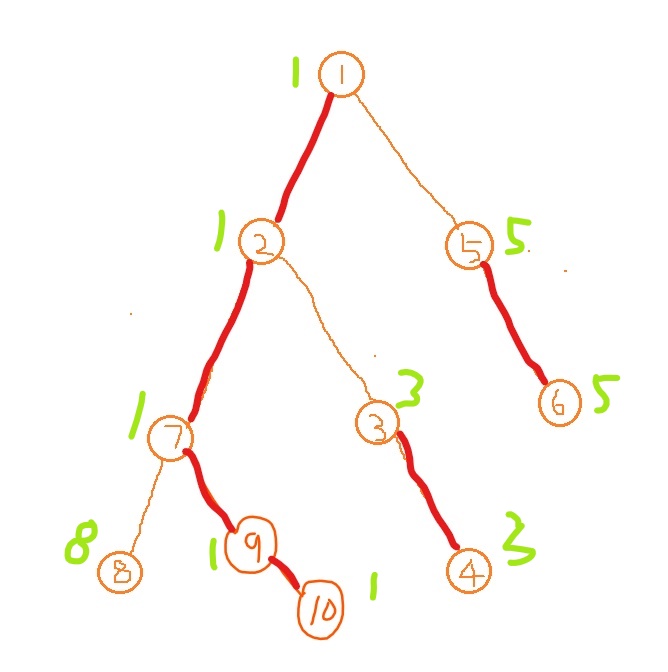
　　  橙边为轻边

　　红边为重边

　　绿数为每个点的 top

　　橙数为每个点的编号

步骤

1　 先预处理 每个点的 deep深度  size子树大小  dad父节点　　

2　 再预处理 每个点的 top重链顶点

3　 就是跳了

应用

洛谷 P2912 [USACO08OCT] 牧场散步

效率蛮高的

此题中用 len[i] 表示 i 到根距离

询问 x 和 y 的距离

答案可用 len[x] + len[y] - 2*len[ lca(x,y) ]表示

而 lca 可以用树剖求出

len[] 在树剖求lca 的预处理中 可以顺带求出来

树剖求 lca 虽然不常用

但它确实很吊

嘻嘻 我的 树剖代码 目前是本题 的 rank1

时间短 空间小

#include<bits/stdc++.h>
#define N 1003
using namespace std;
int cnt,head[N],to[N<<],dis[N<<],next[N<<],len[N],size[N],deep[N],dad[N],n,m,top[N];
int read(){//读入优化
    char ch=getchar();
    int ans=;
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch)){
        ans=ans*+ch-'';
        ch=getchar();
    }
    return ans;
}
int lca(int x,int y){//树剖求lca
    for(;top[x]!=top[y];){
        if(deep[top[x]]<deep[top[y]])x^=y^=x^=y;//利用二进制的 swap()
        x=dad[top[x]];
    }
    if(deep[x]>deep[y])x^=y^=x^=y;
    return x;
}
void dfs(int k){//步骤1
    int v;
    size[k]=,deep[k]=deep[dad[k]]+;
    for(int i=head[k];i;i=next[i]){
        v=to[i];
        if(v!=dad[k])//各种预处理，包括针对本题的 len[]数组
            len[v]=dis[i]+len[k],dad[v]=k,dfs(v),size[k]+=size[v];
    }
}

void dfs1(int k){//步骤2
    int t=,v;
    if(!top[k])top[k]=k;
    for(int i=head[k];i;i=next[i]){
        v=to[i];
        if(v!=dad[k]&&size[t]<size[v])
            t=v;
    }
    if(t)top[t]=top[k],dfs1(t);
    for(int i=head[k];i;i=next[i]){
        v=to[i];
        if(v!=dad[k]&&v!=t)
            dfs1(v);
    }
}
int main(){
    n=read(),m=read();
    int x,y,z;
    while(--n){
        x=read(),y=read(),z=read();
        next[++cnt]=head[x];
        to[cnt]=y;
        head[x]=cnt;
        dis[cnt]=z;
        next[++cnt]=head[y];
        to[cnt]=x;
        head[y]=cnt;
        dis[cnt]=z;
    }
    dfs();
    dfs1();
    while(m--){
        x=read(),y=read();
        printf("%d\n",len[x]+len[y]-(len[lca(x,y)]<<));
    }
    return ;
}