回溯法、DFS

回溯法

为了求得问题的解，先选择某一种可能情况向前探索，在探索过程中，一旦发现原来的选择是错误的，就退回上一步重新选择条件，继续向前探索，如此反复进行，直至得到解或证明无解。

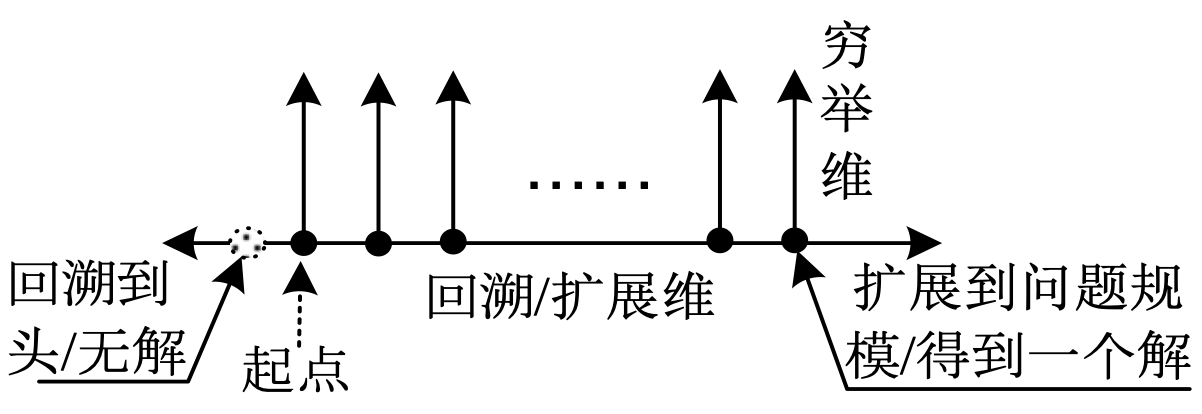
DFS

DFS模板

void dfs(int step)
{
	判断边界
	尝试每一种可能 for (int i=1;i<=n;i++)
	{
		继续下一步 dfs(step+1);
	}
	返回
}

搜索模板的套路：

先判断是否达到目标状态

如果达到，判断当前状态是否合法是否计入答案。

未达到，枚举可能的状态，记录本轮选择，进入下一层。

返回后，消除影响。

例题 全排列(dfs)

#include<bits/stdc++.h>
using namespace std;
int n,a[100],vis[100],t;
void dfs(int cur)
{
	if (cur==n+1)
	{
		for (int k=1;k<=n;k++)
			cout<<a[k];
		cout<<endl;
		t++;
		return ;
	}
	else
	{
		for (int i=1;i<=n;i++)
		{
			if (vis[i]==0)
			{a[cur]=i;
			vis[i]=1;
			dfs(cur+1);
			vis[i]=0;
			}
		}
	}
}
int main()
{
	cin>>n;
	dfs(1);
	cout<<"Total="<<t;
	return 0;
 return 0;
}

输入样例：3

输出样例：

123

132

213

231

312

321