[NOIP2002] 提高组 洛谷P1033 自由落体

题目描述

在高为 H 的天花板上有 n 个小球，体积不计，位置分别为 0，1，2，…．n-1。在地面上有一个小车（长为 L，高为 K，距原点距离为 S1）。已知小球下落距离计算公式为 d＝1/2*g*(t^2)，其中 g=10，t 为下落时间。地面上的小车以速度 V 前进。

如下图：

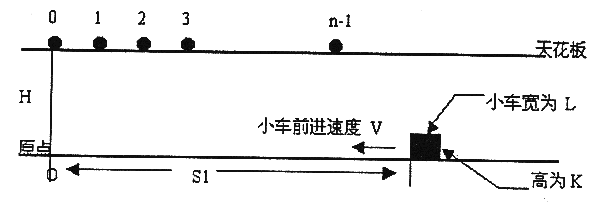
小车与所有小球同时开始运动，当小球距小车的距离 <= 0.0001(感谢Silver_N修正) 时，即认为小球被小车接受（小球落到地面后不能被接受）。

请你计算出小车能接受到多少个小球。

输入输出格式

输入格式：

键盘输人：

H，S1，V，L，K，n （l<=H，S1，V，L，K，n <=100000）

输出格式：

屏幕输出：

小车能接受到的小球个数。

输入输出样例

输入样例#1：

5.0 9.0 5.0 2.5 1.8 5

输出样例#1：

1

物理问题2333

计算小车到达一个位置的时间，和该时间内小球运动的距离，判断能不能接到就行。注意精度误差。

 /*By SilverN*/
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const double eps=0.0001;
 double H,s1,n,L,K,V;
 int main(){
     cin>>H>>s1>>V>>L>>K>>n;
     int cnt=;
     for(int i=;i<n;i++){
         double t=(s1-i)/V;
         double h=*t*t;
         if(H-h<-eps)continue;
         t=(s1+L-i+eps)/V;
         if(H-t*t*-K<=eps)cnt++;
     }
     cout<<cnt<<endl;
     return ;
 }