PAT 1123 Is It a Complete AVL Tree

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

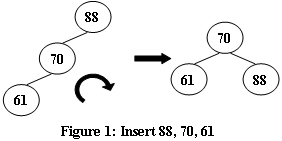
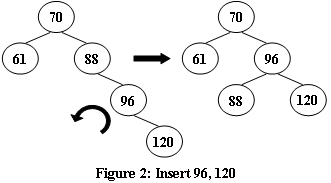
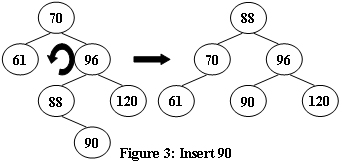
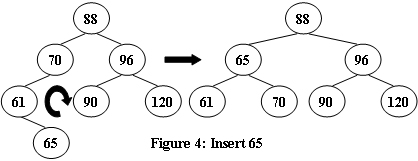
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

Sample Input 1:

5

88 70 61 63 65

Sample Output 1:

70 63 88 61 65

YES

Sample Input 2:

8

88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68

NO

#include<iostream>
#include<math.h>
#include<queue>
using namespace std;
struct node{
	int value, depth;
	node* l=NULL;
	node* r=NULL;
	node(int v): value(v), depth(0), l(NULL), r(NULL){
	}
};
int getheight(node* root){
	return root==NULL?0:max(getheight(root->l), getheight(root->r))+1;
}

node* RotationLL(node* root){
	node* temp=root->l;
	root->l=temp->r;
	temp->r=root;
	temp->depth=getheight(temp);
	root->depth=getheight(root);
	return temp;
} 

node* RotationRR(node* root){
	node* temp=root->r;
	root->r=temp->l;
	temp->l=root;
	temp->depth=getheight(temp);
	root->depth=getheight(root);
	return temp;
}

node* RotationLR(node* root){
    root->l=RotationRR(root->l);
	return RotationLL(root);
}

node* RotationRL(node* root){
	root->r=RotationLL(root->r);
	return RotationRR(root);
}

node* insert(node* root, int val){
	if(root==NULL){
		root=new node(val);
		return root;
	}else if(val<root->value){
		root->l=insert(root->l, val);
		if(getheight(root->l)-getheight(root->r)==2)
			if(val<root->l->value)
				root=RotationLL(root);
			else
				root=RotationLR(root);

	}else{
		root->r=insert(root->r, val);
		if(getheight(root->l)-getheight(root->r)==-2)
			if(val<root->r->value)
				root=RotationRL(root);
			else
				root=RotationRR(root);
	}
	root->depth=getheight(root);
	return root;
}
int main(){
	int n, flag=0, ans=0, first=0;
	cin>>n;
	node* root=NULL;
	for(int i=0; i<n; i++){
		int val;
		cin>>val;
		root=insert(root, val);
	}
	queue<node*> q;
	q.push(root);
	while(!q.empty()){
		node* temp=q.front();
		first++==0?cout<<temp->value:cout<<" "<<temp->value;
		q.pop();
		if(temp->l!=NULL){
			q.push(temp->l);
			flag==1?ans=1:ans=ans;
		}
		else
			flag=1;
		if(temp->r!=NULL){
			q.push(temp->r);
			flag==1?ans=1:ans=ans;
		}
		else
			flag=1;
	}
	cout<<endl;
	ans==1?cout<<"NO"<<endl:cout<<"YES"<<endl;
	return 0;
}