机器学习（2）：简单线性回归 | 一元回归 | 损失计算

前文再续书接上一回，机器学习的主要目的，是根据特征进行预测。预测到的信息，叫标签。

从特征映射出标签的诸多算法中，有一个简单的算法，叫简单线性回归。本文介绍简单线性回归的概念。

（1）什么是简单线性回归

“回归（regression）”是什么？如之前所讲，预测模型可区分为“分类器”跟“回归器”，回归器，就是用来预测趋势变化的，比如预测明天哪支股会涨停，预测某天的降雨量是多少，预测未来一年房价的变化，等等。所以回归就是预测的意思，没有什么高深的。线性是什么意思？就是一条直线，够简单了吧，自然也有“非线性回归”。那“简单”是什么意思，就是只有一个变量的，也叫一元回归，如果是多个变量（拟合面），那就叫多元回归（自然不再是简单线性）。

所以，简单线性回归，就是只有一个输入变量（自变量）的预测，就是这一种：y=ax+b，根据x的值，预测出y。你可以说，简单线性回归，就是一个函数。

简单线性回归是一个预测模型（回归模型），是模型就要被训练，只有不断的训练才能得到最佳的预测状态--虽然这是废话，但的确是这样。同样，简单线性回归的目的，是尽可能拟合所有训练样本以达到最佳的预测状态。什么是拟合？比如画一条直线，尽可能地，让各个点（样本）的预测标签接近或重合实际标签，就是拟合。

为了更好的解释这个概念，我画了一个图，图上面解释了相关概念：

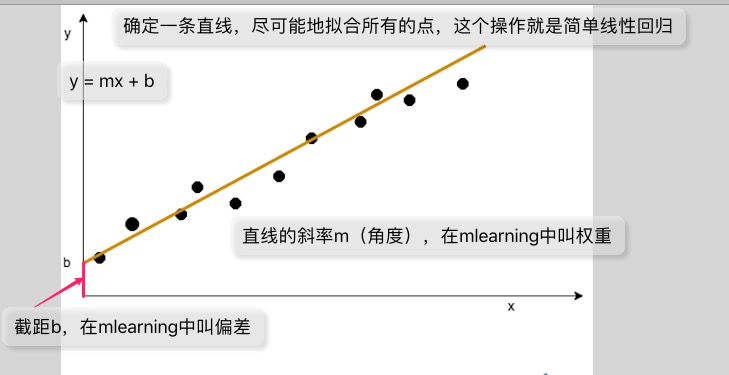
从图上可以看到，如果对于每个点的输入特征，得到的预测标签跟这个点的实际标签都能重合的话，那就是最佳的。然而，实际上很可能做不到所有点都落在直线上，那这时候，找出一点最佳的直线，获得最好的拟合效果，就是机器学习要做的事情。

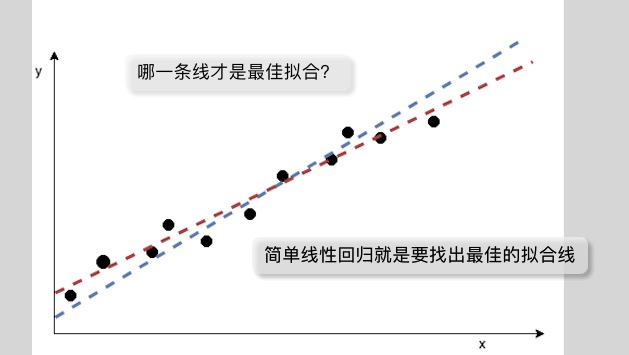
简单线性回归模型，给出了特征与标签的关系：

y = mx + b

x是输入特征，y是预测标签。

为了让这条直线更好的拟合所有的点，就要调整参数m跟b。

m是直线的角度，叫斜率，在机器学习中叫权重。

b叫截距，在机器学习中叫偏差。

所以，使用简单线性回归算法，机器学习通过大量带标签的样本进行训练，最终调整出一个最佳的m跟b值，从而达到最好的拟合效果。

那么，怎么判断拟合效果呢？怎么知道是变好还是变差了？

（2）如何判断拟合效果

为了判断拟合的效果，这里引入一个概念，叫损失计算。

如果点刚好落在直线上，也就是预测标签跟实际标签一样，那损失为0。

而实际上，更多的情况下，损失并不为0，这时要考虑整体损失。

整体损失越小，拟合越好，比如下图所示，可以明显分辨出左线的拟合效果优于右线（当整体损失达到某个值时，就可以认为已经取得很好的预测效果，可以停止训练）：

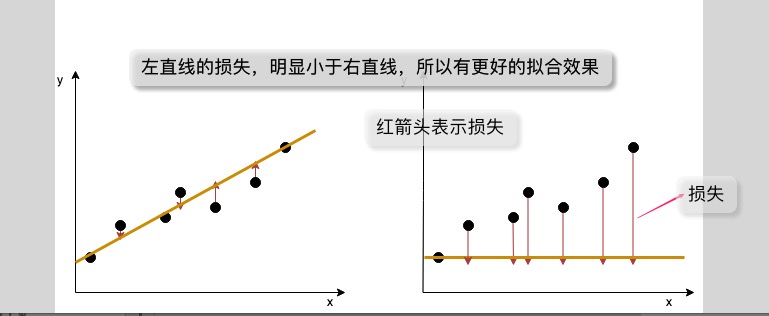
上图中，每个点跟预测标签的距离（也就是点到线的红箭头）称为损失。

整体损失的计算可以有很多办法，这里引入一个简单实用的办法：均方误差（MSE）。

均方误差（MSE），就是求出所有点的损失的平方和，再除以样本的个数。你可以参考这个图的解释：

以上这个图，来源于这个地址：https://developers.google.com/machine-learning/crash-course/descending-into-ml/training-and-loss

基本上，本文的内容与组织方式，都跟这个地址的教程有直接的关系。

以上介绍了简单线性回归的定义，以及损失计算的一个办法即MSE，接下来小程用实例来演示简单线性回归的实现。

（3）简单线性回归示例

这里以python来演示，主要是因为python易于使用。

首先，给定一些散列的点，你可以参考下图的实现，截图中对部分代码做了解释：

执行这一部分代码，可以看到这样的效果：

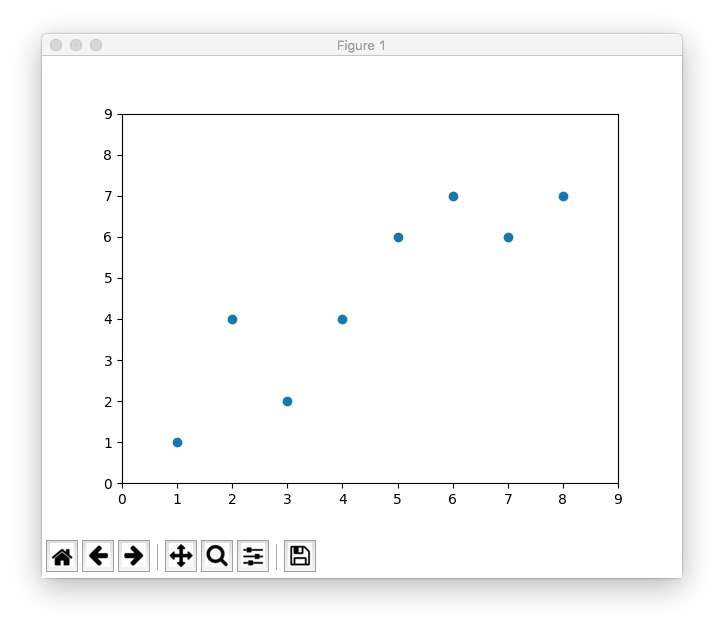
然后，对这些点进行简单线性回归，也就是画一条拟合线，并取得最好的拟合效果，参考下图：

最终执行的效果是这样的：

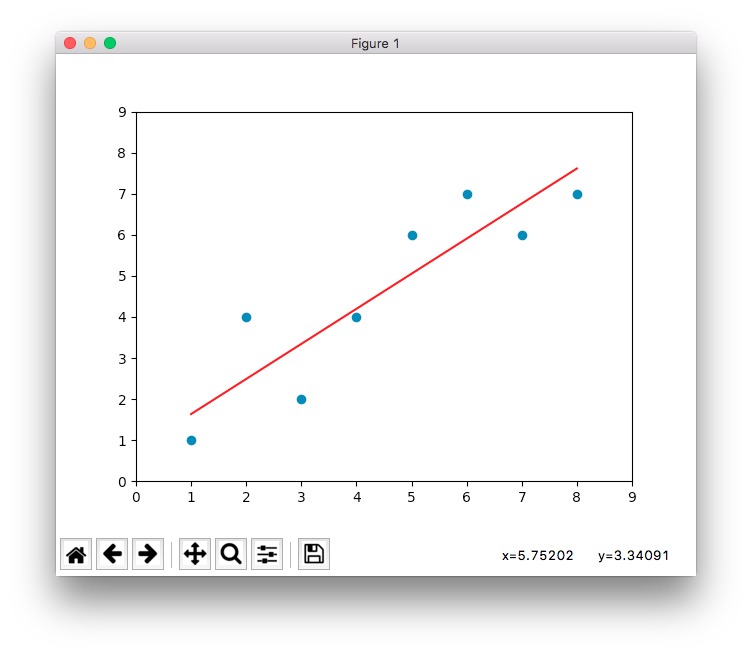
好了，回头看一下吧。本文介绍了简单线性回归的定义以及损失计算的一个办法即MSE，最后用python示范了怎么使用简单线性回归算法绘制一条拟合线。简单线性回归，就是一个预测模型，更直接一点，就是一个函数--你可以说预测模型其实就是函数，就是一个算法设计（比如y=ax+b就是一个最核心的东西），它接受训练后的进化（比如不断地调整参数），从而得到最佳的预测状态。