【计算几何】二维凸包——Graham's Scan法

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const int maxn= ;

 struct _point
 {
     double x, y;
     _point (double _x= , double _y= )
     {
         x= _x;
         y= _y;
     }
     /*friend: 修饰词：友元函数*/
     friend inline _point operator + (const _point &a, const _point &b)
     {
         return _point(a.x+ b.x, a.y+ b.y );
     }
     friend inline _point operator - (const _point &a, const _point &b)
     {
         return _point(a.x- b.x, a.y- b.y );
     }
     friend inline double operator * (const _point &a, const _point &b)
     {
         /*叉乘，求叉积*/
         /*x1y2- x2y1*/
         return (a.x* b.y)- (b.x* a.y);
     }
 };
 _point point[maxn];
 _point In_Bag[maxn];

 double getDis(_point a,_point b)
 {
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 }
 bool cmpx (const _point &a,const _point &b)
 {
     /*极角按逆时针排序（顺时针的点排在前面便是逆时针排序）*/
     /*叉积等于0，两向量平行*/
     double k= (a- point[])* (b- point[]);
     return == k? (getDis(a, point[])- getDis(b, point[])<= ): k< ;
 }

 int cnt; //凸包集里点的个数;
 void Graham_Scan(int n)
 {
     cnt= -;
     In_Bag[++ cnt]= point[];
     for(int i= ; i< n; i ++)
     {
         while(cnt&& (point[i]- In_Bag[cnt])* (In_Bag[cnt]-In_Bag[cnt- ])<  )
         {
             /*当In_Bag中至少有基点和另一点时(cnt>= 1)*/
             /*逆时针扫描时，如果向量{pn- 1, pn}与{pn, pn+ 1}的叉积为负，则将上一点删除*/
             /*顺时针扫描判断是否为正*/
             -- cnt;
         }
         In_Bag[++ cnt]= point[i];
     }
 }

 int main()
 {
     int n;
     double xx, yy;
     while (~ scanf("%d", &n))
     {
         for (int i= ; i< n; i ++)
         {
             scanf("%lf %lf", &xx, &yy);
             if (i)
             {
                 if (yy< point[].y|| (yy== point[].y&& xx< point[].x))
                 {
                     double tmp= yy;
                     yy= point[].y;
                     point[].y= tmp;
                     tmp= xx;
                     xx= point[].x;
                     point[].x= tmp;
                 }
             }
             point[i].x= xx;
             point[i].y= yy;
         }
         sort(point+ , point+ n, cmpx);
         Graham_Scan(n);

         /*求凸包周长*/
         double Dis= ;
 //        cout << "********************" << endl;
 //        for (int i= 0; i<= cnt; i ++)
 //        {
 //            cout << In_Bag[i].x << " " << In_Bag[i].y << endl;
 //        }
         for (int i= ; i<= cnt; i ++)
         {
             Dis+= getDis(In_Bag[i], In_Bag[(i+ )% (cnt+ )]);
         }
         printf("%.2f\n", Dis);
     }
     return ;
 }

简化后模板

凸包

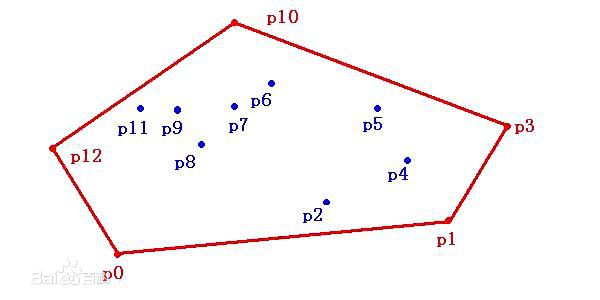
点集Q的凸包（convex hull）是指一个最小凸多边形，满足Q中的点或者在多边形边上或者在其内。右图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包。

一组平面上的点，求一个包含所有点的最小的凸多边形，这就是凸包问题了。这可以形象地想成这样：在地上放置一些不可移动的木桩，用一根绳子把他们尽量紧地圈起来，并且为凸边形，这就是凸包了。

数学定义：设S为欧几里得空间Rⁿ的任意子集。包含S的最小凸集称为S的凸包，记作conv(S)。

【百度百科】https://baike.baidu.com/item/%E5%87%B8%E5%8C%85/179150?fr=aladdin

以下内容基本照搬。

凸包最常用的凸包算法是Graham扫描法和Jarvis步进法

①Graham's Scan法

这个算法是由数学大师葛立恒（Graham）发明的。

⒈ 在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。坐标相同的点应排除。

2.然后按照其它各点p和基点构成的向量<H,p>；与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据余弦定理求出向量夹角的余弦值即可。

以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

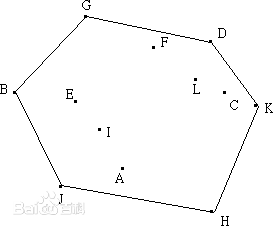
3.线段<H,K>；一定在凸包上，接着加入C。假设线段<K,C>；也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K,D>；才会在凸包上，所以将线段<K,C>；排除，C点不可能是凸包。即当加入一点时，必须考虑到前面的线段是否在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为Pn+1，上一点为Pn，再上一点为P_n-1 。顺时针扫描时，如果向量{P_n-1 ,Pn}与{Pn,Pn+1}的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

4.在上图中，加入K点时，由于线段<H,C>要旋转到<H,K>的角度，为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K,D>要旋转到<H,K>的角度，为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍历完成，即得到凸包。

向量的叉积

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。

两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。

向量积|c|= |a×b|= |a||b|sin<a，b>；c的方向遵守右手定则。c是垂直a、b所在平面，且以|b|·sinθ为高、|a|为底的平行四边形的面积。

c = a×b=(x1y2- x2y1);

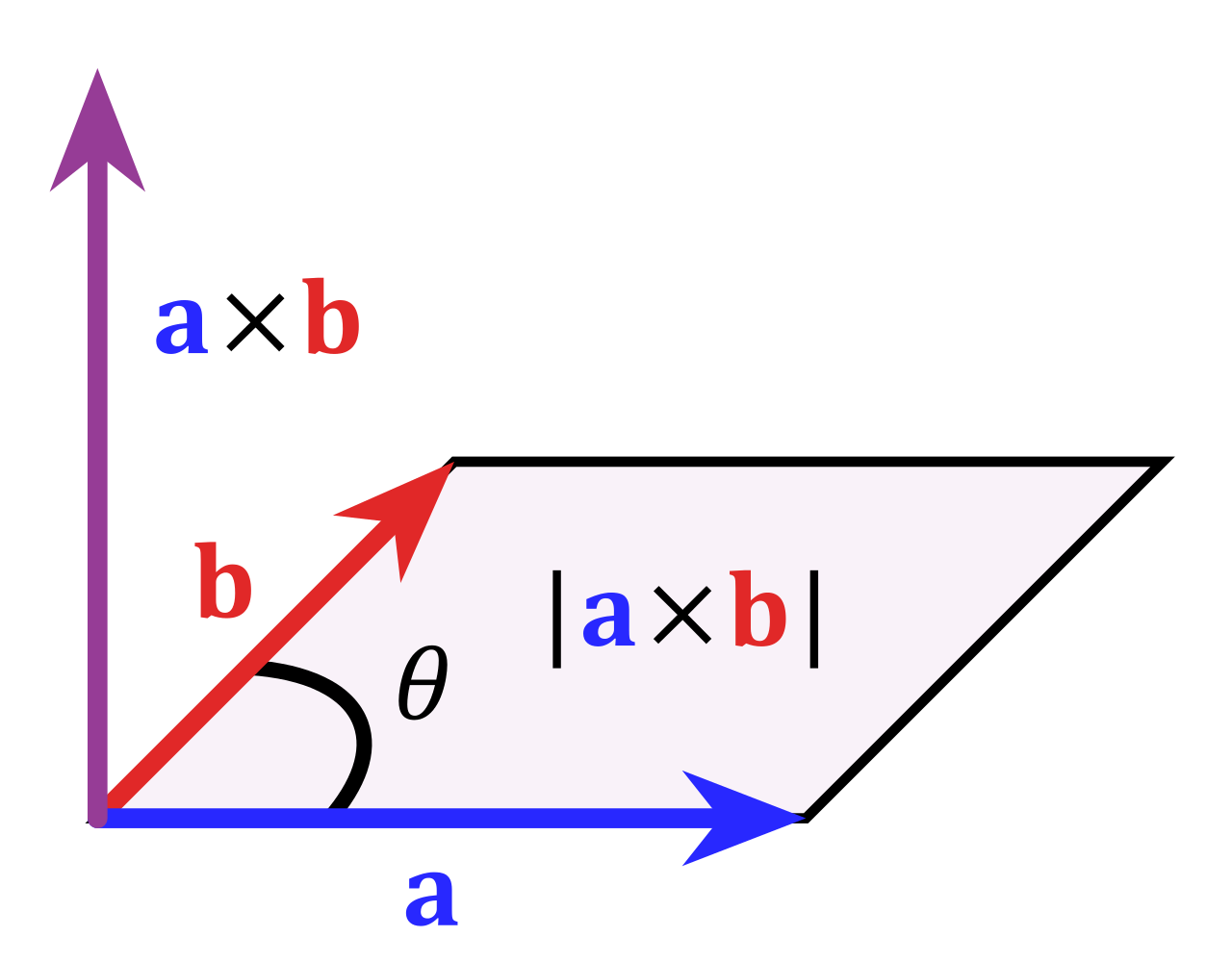
【图源维基百科】

维基百科中向量积解释：https://en.wikipedia.org/wiki/Cross_product

下面放一个例子吧；

【洛谷】P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

题目描述

农夫约翰想要建造一个围栏用来围住他的奶牛，可是他资金匮乏。他建造的围栏必须包括他的奶牛喜欢吃草的所有地点。对于给出的这些地点的坐标，计算最短的能够围住这些点的围栏的长度。

输入格式：

输入数据的第一行包括一个整数 N。N（0 <= N <= 10,000）表示农夫约翰想要围住的放牧点的数目。接下来 N 行，每行由两个实数组成，Xi 和 Yi,对应平面上的放牧点坐标（-1,000,000 <= Xi,Yi <= 1,000,000）。数字用小数表示。

输出格式：

输出必须包括一个实数，表示必须的围栏的长度。答案保留两位小数。

这是一道二维凸包模板题。我按上面的步骤一点点拆分一下。

首先两个pair数组，分别存放所有的点和位于凸包上的点。

const int maxn = ;
typedef pair<double, double> _pair;

_pair point[maxn];
_pair In_Bag[maxn];

之所以用pair是因为二维坐标刚好两个点，有便宜不占嘿嘿嘿。

然后一些基本的计算几何公式；

计算两点间距离。

double Get_Dis (_pair point1, _pair point2)
{
    //计算两点间距离
    return sqrt(((point1.first- point2.first)* (point1.first- point2.first) )
                + ((point1.second- point2.second)* (point1.second- point2.second) ) );
}

计算叉积。

double Get_axb (_pair a_point1, _pair a_point2, _pair b_point1, _pair b_point2)
{
    //计算两条向量的叉积
    //向量a= a_point1 --> a_point2= a_point2- a_point1;
    //向量b= b_point1 --> b_point2= b_point2- b_point1;
    //叉积axb= (a.x* b.y)- (b.x* a.y);
    //a.x= a_point2.x- a_point1.x; a.y= a_point2.y- a_point1.y;
    return (((a_point2.first- a_point1.first)* (b_point2.second- b_point1.second) )
            - ((b_point2.first- b_point1.first)* (a_point2.second- a_point1.second) ) );
}

计算向量a和x轴所成角的余弦值。

double Get_Cos (_pair point1, _pair point2)
{
    //计算向量a(point1-->point2) 的余弦值;
    point2.first-= point1.first;                //把point1看作坐标原点(0, 0);
    point2.second-= point1.second;              //则point2的坐标为(P2.x- P1.x, P2.y- P1.y);
    point1.first= ;
    point1.second= ;
    _pair point3;                               //在X轴上找一点P3,做直角三角形;
    point3.first= point2.first;                 //P3.x= P2.x;
    point3.second= ;                           //P3.y= P1.y= 0;
    double Dis_P1_P2= Get_Dis(point1, point2);  //计算直角三角形的斜边长,即P1P2之间的距离;
    return point3.first/ Dis_P1_P2;             //邻边/ 斜边;
}

确定了基点后，围绕基点对其余点排序（按余弦值），判断函数cmp。

bool cmpx_1 (_pair a, _pair b)
{
    //小于运算(按与基点P0所成向量的余弦值大小,余弦值越大越优先;cosx在[0,Pi]内从1到-1，减函数；
    //排序后,按逆时针方向遍历点集;
    _pair tmp = point[];                       //基点;
    double Cos_a = Get_Cos(tmp, a);             //求出a,b的余弦值;
    double Cos_b = Get_Cos(tmp, b);
    return Cos_a- Cos_b> ;                     //余弦值越大越优先(越大逆时针遍历越靠前);
}

主函数中，在输入时先确定基点point[0]，然后对其余点按逆时针顺序排序。

for (int i = ; i < n; i ++)
{
    cin >> x >> y;
    if (i )
    {
        if (y< point[].second|| (y== point[].second&& x< point[].first) )
        {
            double tmp= y;
            y= point[].second;
            point[].second= tmp;
            tmp= x;
            x= point[].first;
            point[].first= tmp;
        }
    }
    point[i].first= x;
    point[i].second= y;
}
sort(point+ , point+ n, cmpx_1);

对排序后的点集，判断是否加入In_Bag[]。

int cnt= -;                          //cnt -->In_Bag[]中最后一位元素的数组下标;
In_Bag[++ cnt]= point[];
for (int i = ; i < n; i ++)          //从point[1]开始;
{
    while (cnt&& Get_axb(In_Bag[cnt- ], In_Bag[cnt], In_Bag[cnt], point[i])<  )
    {
        //当In_Bag中至少有基点和另一点时(cnt>= 1时);
        //逆时针扫描时,如果向量{Pn-1, Pn}与{Pn, Pn+1}的叉积为负,则将上一点删除;
        //(顺时针扫描判断是否为正)
        -- cnt;
    }
    In_Bag[++ cnt]= point[i];
}

最后把所有点首尾相连，算出距离和即可。

double Dis = ;
for (int i= ; i<= cnt; i ++)
{
    Dis+= Get_Dis(In_Bag[i], In_Bag[(i+ )% (cnt+ )]);
}
printf("%.2f\n", Dis);

谢谢各位能看到最后嘿嘿。

完整的代码在这里。

https://www.cnblogs.com/Amaris-diana/p/10519865.html