bzoj3884: 上帝与集合的正确用法（数论）

　　感觉是今天洛谷月赛T3的弱化版，会写洛谷T3之后这题一眼就会写了...

　　还是欧拉扩展定理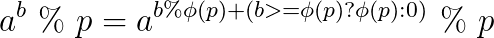

　　于是就在指数上递归%phi(p)+phi(p)直到1，则后面的指数就都没用了，这时候返回，边回溯边快速幂。因为一个数最多求log次phi就变成1，所以复杂度为O(logp*sqrt(p))，这题线性筛是比直接求要慢的...

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=,inf=1e9;
int T,x;
int p[maxn];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
inline int phi(int x)
{
    int ans=x;
    for(int i=;i*i<=x;i++)
    if(!(x%i))
    {
        ans=ans/i*(i-);
        while(!(x%i))x/=i;
    }
    if(x>)ans=ans/x*(x-);
    return ans;
}
inline int power(int a,int b,int mod)
{
    if(!a)return ;int ans=;
    for(;b;b>>=,a=1ll*a*a%mod)
    if(b&)ans=1ll*ans*a%mod;
    return ans;
}
int solve(int mod)
{
    if(mod==)return ;int tmp;
    return power(,solve(tmp=phi(mod))+tmp,mod);
}
int main()
{
    read(T);
    while(T--)read(x),printf("%d\n",solve(x));
    return ;
}