codeforces 477B B. Dreamoon and Sets(构造)

题目链接：

B. Dreamoon and Sets

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon likes to play with sets, integers and 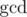.  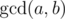is defined as the largest positive integer that divides both a and b.

Let S be a set of exactly four distinct integers greater than 0. Define S to be of rank k if and only if for all pairs of distinct elements si, sjfrom S, .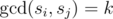

Given k and n, Dreamoon wants to make up n sets of rank k using integers from 1 to m such that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum m that makes it possible and print one possible solution.

Input

The single line of the input contains two space separated integers n, k (1 ≤ n ≤ 10 000, 1 ≤ k ≤ 100).

Output

On the first line print a single integer — the minimal possible m.

On each of the next n lines print four space separated integers representing the i-th set.

Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal m, print any one of them.

Examples

input

1 1

output

5
1 2 3 5

input

2 2

output

22
2 4 6 22
14 18 10 16

题意：

构造n个集合,每个集合里面4个数,每两个数的gcd=k,问这些数里面的最大的那个数最小是多少,和这些集合是怎样的;

思路：

1,2,3,5   7,8,9,11,  13,14,15,17 就是这样的规律,跟原来那个什么6*n+1，6*n+5折两个数有可能是质数一样，每6个相邻的数里面两两互质的就是6*n+1,6*n+2,6*n+3,6*n+5了;
然后乘上k就好了;

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <bits/stdc++.h>
#include <stack>
#include <map>

using namespace std;

#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));

typedef  long long LL;

template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('\n');
}

const int mod=1e9+7;
const double PI=acos(-1.0);
const int inf=1e9;
const int N=1e6+20;
const int maxn=1e5+110;
const double eps=1e-12;

int main()
{
    int n,k;
    read(n);read(k);
    cout<<(n-1)*6*k+5*k<<endl;
    For(i,1,n)
    {
        int t=(i-1)*6+1;
        printf("%d %d %d %d\n",t*k,t*k+k,t*k+2*k,t*k+4*k);
    }

    return 0;
}