2014 Super Training #4 G What day is that day? --两种方法

原题： ZOJ 3785 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3785

题意：当天是星期六，问经过1^1+2^2+3^3....+n^n天后是星期几？

这题开始以为是这种式子的求和问题，翻了半天没翻到公式。结果没搞出来。后来发现有两种方法。

第一种方法： 找规律

打表可以看出，这些数的结果出现42一循环，所以直接就处理出前42个，后面的就用前面的。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
using namespace std;
#define N 20007

int sum[];
string ss[] = {"Saturday","Sunday","Monday","Tuesday","Wednesday","Thursday","Friday"};\

void init()
{
    int n,i,j;
    sum[] = ;
    for(n=;n<=;n++)
    {
        int flag = n%;
        int ans = ;
        for(j=;j<=n;j++)
            ans = (ans*flag)%;
        sum[n] = ans;
    }
    for(i=;i<=;i++)
        sum[i] += sum[i-];
}

int main()
{
    int i,j,t,n,ans;
    init();
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        ans = (((n/)%*(sum[]%))% + sum[n%]%)%;
        cout<<ss[ans]<<endl;
    }
    return ;
}

第二种方法： 矩阵乘法

先把底数对7取模，得出1^1+1^8+1^15+...+ 2^2+2^9+2^16+...

然后就可以分成7组，分别用矩阵加速计算结果，关键就在矩阵的构造了，这个构造我也没太搞懂：

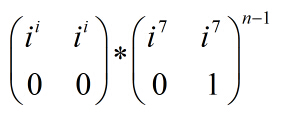    摘自AB的博客。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 107

char s[][]={"Saturday","Sunday","Monday","Tuesday","Wednesday","Thursday","Friday"};

struct Matrix
{
    int m[][];
};

Matrix Mul(Matrix a,Matrix b)
{
    Matrix c;
    memset(c.m,,sizeof(c.m));
    for(int i=;i<;i++)
        for(int j=;j<;j++)
            for(int k=;k<;k++)
                c.m[i][j] += ((a.m[i][k]*b.m[k][j])% + )%;
    return c;
}

int fastm(int a,int b)
{
    int res = ;
    while(b)
    {
        if(b&)
            res = (res*a)%;
        a = (a*a)%;
        b >>= ;
    }
    return res;
}

Matrix MPow(Matrix &res,Matrix a,int n)  //第二种写法
{
    while(n)
    {
        if(n&)
            res = Mul(res,a);
        n>>=;
        a = Mul(a,a);
    }
    return res;
}

int main()
{
    Matrix res,tmp;
    int t,n,i;
    int sum,num;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        sum = ;
        for(i=;i<=;i++)
        {
            res.m[][] = res.m[][] = fastm(i,i)%;
            res.m[][] = res.m[][] = ;
            tmp.m[][] = tmp.m[][] = fastm(i,)%;
            tmp.m[][] = ;
            tmp.m[][] = ;
            num = n/;
            if(n% >= i)
                num++;
            if(num > )
            {
                num--;
                MPow(res,tmp,num);
                sum = (sum + res.m[][])%;
            }
        }
        printf("%s\n",s[sum]);
    }
    return ;
}