Fisher线性判别分析(二分类)
LDA(Linear Discriminant Analysis)是一种经典的线性判别方法,又称Fisher判别 分析。该方法思想比较简单:给定训练集样例,设法将样例投影到一维的直线 上,使得同类样例的投影点尽可能接近和密集,异类投影点尽可能远离。
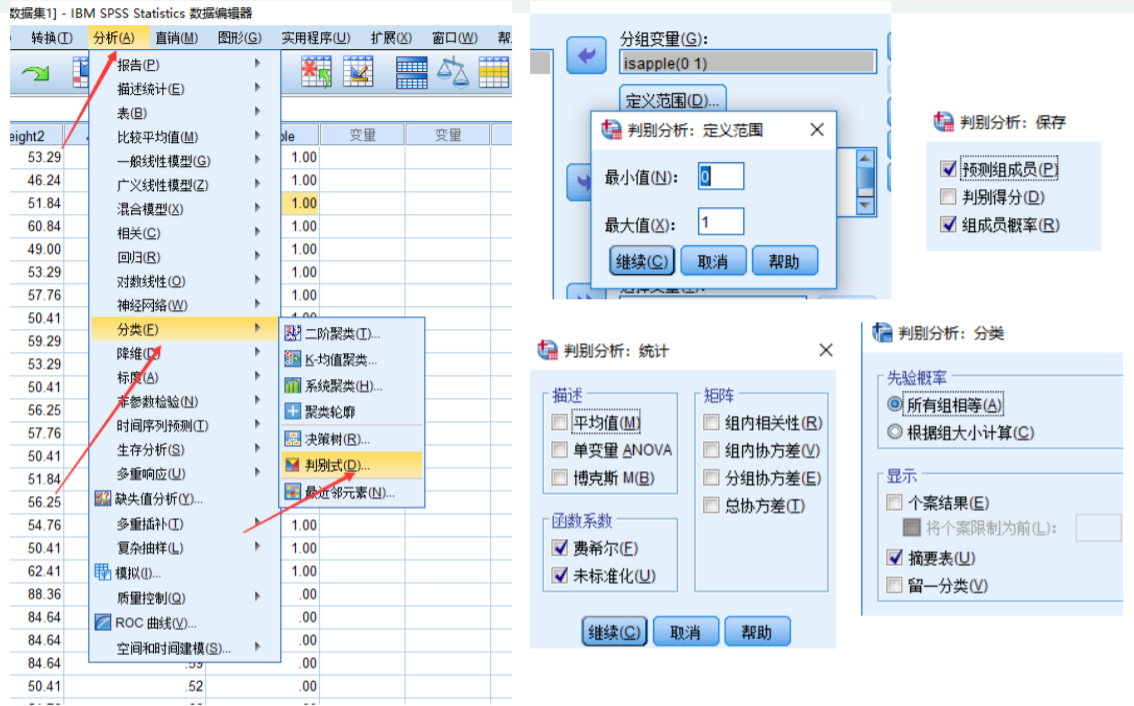
核心问题:找到线性系数向量
结果分析

Fisher判别分析可用于多分类
Logistic回归也可用于多分类

Fisher线性判别分析(二分类)的更多相关文章
- Fisher线性判别分析
Fisher线性判别分析 1.概述 在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口. 假设数据存在于d ...
- 主成分分析(PCA)与线性判别分析(LDA)
主成分分析 线性.非监督.全局的降维算法 PCA最大方差理论 出发点:在信号处理领域,信号具有较大方差,噪声具有较小方差 目标:最大化投影方差,让数据在主投影方向上方差最大 PCA的求解方法: 对样本 ...
- 线性判别分析(LDA)准则:FIsher准则、感知机准则、最小二乘(最小均方误差)准则
准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...
- 线性判别分析(Linear Discriminant Analysis)转载
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- 线性判别分析算法(LDA)
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- (数据科学学习手札17)线性判别分析的原理简介&Python与R实现
之前数篇博客我们比较了几种具有代表性的聚类算法,但现实工作中,最多的问题是分类与定性预测,即通过基于已标注类型的数据的各显著特征值,通过大量样本训练出的模型,来对新出现的样本进行分类,这也是机器学习中 ...
- 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)
在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...
- matlab 实现感知机线性二分类算法(Perceptron)
感知机是简单的线性分类模型 ,是二分类模型.其间用到随机梯度下降方法进行权值更新.参考他人代码,用matlab实现总结下. 权值求解过程通过Perceptron.m函数完成 function W = ...
- 线性判别分析(LDA), 主成分分析(PCA)及其推导【转】
前言: 如果学习分类算法,最好从线性的入手,线性分类器最简单的就是LDA,它可以看做是简化版的SVM,如果想理解SVM这种分类器,那理解LDA就是很有必要的了. 谈到LDA,就不得不谈谈PCA,PCA ...
- 机器学习中的数学-线性判别分析(LDA), 主成分分析(PCA)
转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html 版权声明: 本文由L ...
随机推荐
- V8是如何执行JavaScript代码的?
前言 一般来讲,电脑是不能直接运行我们的javascript代码的,它需要一个翻译程序将人类能够理解的编程语言 JavaScript,翻译成机器能够理解的机器语言.目前市面上有很多种 JavaScri ...
- 【了解LLM】—— LLM&& SD 基本概念
本文地址:https://www.cnblogs.com/wanger-sjtu/p/17417312.html Causual LM 这里以llama模型为例,通常在执行用户输入之前会有一个[[文章 ...
- Auto.js食用指南
Auto.js食用指南 控件点击是autojs特有的一项功能,基于安卓的无障碍功能的,在软件上有很好的支持,常用于办公软件等...... 前言: 软件选择: auto.js 8.0pro版本(对比4. ...
- Electron App 安装包定制 -- Inno Setup 脚本 Pascal Scripting 初探
在做 Electron 项目时,有个需求是安装包安装时要给客户机上装上某个软件 在查看 Inno Setup 官网后发现是通过 .iss 脚本编写实现自定义安装过程 可在 .iss 内可以添加脚本为安 ...
- (内附示例源码)如何通过electron构建桌面跨平台音视频应用
近年来,视频直播.直播带货.在线教育.在线医疗等音视频领域的相关行业都非常热门,成为大众瞩目的焦点. 在不久的将来,音视频技术渗透于各行各业,无处不在.从IoT网络到个人用户的移动设备,音视频技术以不 ...
- 快速切换 nodejs 的版本
最近在开发一个常驻进程.定时任务统一调度系统,以应对开发在进程管理方面遇到的各种复杂问题. 组里开发项目,一般来说是一个人承包整个项目,包括调度器设计,还有后台系统.我还有一部分工作,是队列相关的信息 ...
- Django reset framework: 序列化
序列化与反序列化 将模型转换为json 称之为 序列化 将json转换为模型 称之为 反序列化 何时进行序列化与反序列化 序列化:当后端将数据库中信息取出返回给前端时,要进行序列化操作 反序列化:当需 ...
- [linux]搭建nfs
环境 说明 IP 系统版本 服务端 192.168.137.7 centos 7 客户端 192.168.137.8 centos 7 步骤 配置服务端 安装 nfs 服务 yum install - ...
- vscode snnipet of python
{ // Place your snippets for python here. Each snippet is defined under a snippet name and has a pre ...
- 自治系统/自治域和自治系统编号(ASN)
定义: 自治系统或自治域(英文:Autonomous system, AS)是指在互联网中,一个或多个实体管辖下的所有IP网络和路由器的组合,它们对互联网执行共同的路由策略.参看RFC 1930中更新 ...
