一个vuepress配置问题，引发的js递归算法思考

前言

这两天在尝试用语雀＋ vuepress ＋ github 搭建个人博客。

小破站地址 ：王天的 web 进阶之路

语雀作为编辑器，发布文档推送 github，再自动打包部署，大概流程如下。

问题

我使用的elog插件批量导出语雀文档。elog采用的配置是所有文章平铺导出，没有按照语雀知识库目录生成markdown，这导致 vuepress 侧边栏无法和语雀一致，如下图。

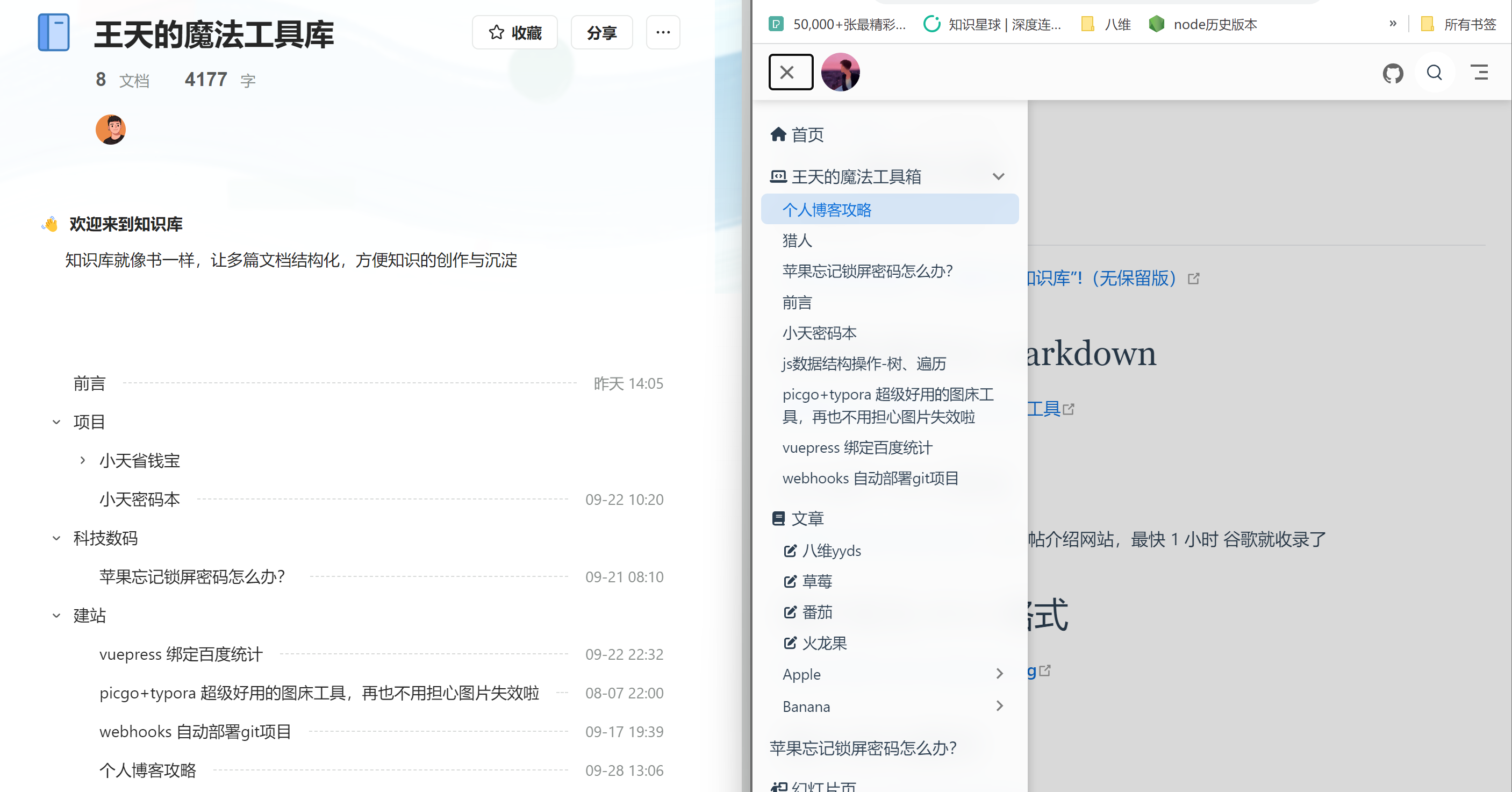
上图，左侧是语雀知识库，右侧是导出到 vuepress 展示的效果，很明显没有目录这很影响阅读体验呀

解决

在查阅 vuepress 文档后，发现配置silderbar.ts可以自定义侧边栏目录，配置参数如下：

export default {
  theme: defaultTheme({
    // 可折叠的侧边栏
    sidebar: {
      "/web/": [
        {
          text: "王天的web进阶手册",
          collapsible: true, // 目录是否折叠
          children: ["/reference/cli.md", "/reference/config.md"], // 文档目录
        },
        {
          text: "王天的魔法工具箱",
          collapsible: true,
          children: [
            "/reference/bundler/vite.md",
            "/reference/bundler/webpack.md",
          ],
        },
      ],
    },
  }),
};

递归生成菜单

配置sidebar.ts 可以修改左侧菜单，但是一个个手动修改这忒麻烦了啊啊啊啊。那如何批量生产菜单配置项呢？

递归函数呀呀呀呀呀呀

elog 在同步语雀文档时，会自动创建elog.cache.json缓存文件，在 vueprss 项目根目录中查看。

打开elog.cache.json文件，我们能看到语雀文档知识库的数据结构

"catalog": [
    {
      "type": "DOC",
      "title": "前言",
      "uuid": "17Os-_V_hcS37KOD",
      "url": "wqbpyf5083qc7ho8",
      "prev_uuid": "",
      "sibling_uuid": "dmQSRn6AXUBSg96x",
      "child_uuid": "",
      "parent_uuid": "",
      "doc_id": 141216125,
      "level": 0,
      "id": 141216125,
      "open_window": 1,
      "visible": 1
    }
  ]

catlog 属性是文档缓存数据，关键字段：

• type：值为'DOC' 是文章、值为 TITLE 则为目录
• uuid：文章 id
• prent_uuid:父节点的 uuid

咱们根据以上参数，编写递归函数， 将elog.cache.json的一维数组，递归生成 vuepress 侧边栏配置数据

代码如下：

function genYuqueRoute() {
  // 参数1:遍历数组
  // 参数2:父菜单id
  const deep = (arrlist, parantId) => {
    let forList: any[] = [];
    arrlist.forEach((element) => {
      // 菜单id不一致，跳出循环调用
      if (element.parent_uuid !== parantId) return;
      // 如果是TITLE类型新增配置项
      if (element.type === "TITLE") {
        forList.push({
          text: element.title,
          collapsible: true,
          children: deep(arrlist, element.uuid),
        });
        // 如果是DOC 类型追加文件地址
      } else {
        forList.push(element.url + ".md");
      }
    });
    return forList;
  };
  return deep(catalog, "");
}

效果

敲重点啦！

递归函数本质上是一个在回调自身的函数，用于改造数据结构，重点在于跳出循环的机制，否则陷入死循环啦

DFS vs BFS ？

什么是 DFS 、BFS ?

• DFS 深度优先搜索：可以用于找到一条路径、判断图中是否存在循环、拓扑排序、生成连通分量等。
• BFS 广度优先搜索：可以用于找到最短路径、生成最小生成树、进行网络分析等。

:::danger

‍♀️ 简单理解为，横向 、竖向 遍历据状结构

• 深度优先搜索，对数据结构的横向执行，从第一行遍历子节点、叶子节点，依次直到最后一行。
• 广度优先搜索，对数据结构的竖向执行，把树结构平面铺开、以层级数为列数，从第一列依次执行。
  
  :::

将深度搜索、广度搜索代入到生活场景更容易理解。

咱们先看一个家庭关系树状图，爷爷奶奶是一级属性、父母叔伯二级、孙子孙女三级属性、重孙们是四级属性，以此类推。形成一个家庭关系树状图。

假如奶奶过八十大寿，按辈分来，首先是父母叔伯这一辈祝寿，其次是孙子孙女辈分，最后重孙们，以此类推，这个竖向执行的祝寿过程就是广度优先搜索

那过年走亲戚的话，咱们没有俺辈分，去分批的吧？至少我们老家不是的，都是一去一家子呢。那这个横线执行的过程，就是深度优先搜索。

深度优先搜索（DFS）示例代码：

从 A 节点依次取出数据

// 图的邻接表表示
const graph = {
  A: ["B", "C"],
  B: ["D", "E"],
  C: ["F", "G"],
  D: [],
  E: [],
  F: [],
  G: [],
};

// 使用深度优先搜索遍历图
function dfs(graph, start) {
  const visited = new Set(); // 存储已访问节点的集合

  function traverse(node) {
    visited.add(node); // 将当前节点标记为已访问
    console.log(node); // 打印遍历的节点

    const neighbors = graph[node]; // 获取当前节点的邻居节点
    for (const neighbor of neighbors) {
      // 遍历当前节点的邻居节点
      if (!visited.has(neighbor)) {
        // 如果邻居节点未被访问过
        traverse(neighbor); // 递归遍历邻居节点
      }
    }
  }

  traverse(start); // 从起始节点开始进行深度优先搜索
  return visited; // 返回所有已访问的节点
}

输出结果：

dfs(graph, "A"); // 对图进行深度优先搜索，从起始节点 'A' 开始，并打印遍历结果
// A
// B
// D
// E
// C
// F
// G

在上述代码中，图使用邻接表表示，dfs 函数使用递归方式实现了深度优先搜索。从起始节点 'A' 开始，递归访问其邻居节点，并在访问时输出节点的值。

广度优先搜索（BFS）示例代码：

// 广度搜索 BFS
let graph = {
  A: ["B", "C"],
  B: ["A", "C", "D"],
  C: ["A", "D", "E"],
  D: ["B", "C", "E"],
  E: ["C", "D", "F"],
  F: ["E", "W"],
  W: ["C"],
};

function bfs(graph, startPoint) {
  let queue = []; // 用于存储待访问节点的队列
  let result = []; // 存储遍历结果的数组

  queue.push(startPoint); // 将起始节点添加到队列
  result.push(startPoint); // 将起始节点添加到遍历结果

  while (queue.length > 0) {
    // 当队列不为空时进行循环
    let point = queue.shift(); // 取出队列中的第一个节点作为当前节点
    let nodes = graph[point]; // 获取当前节点的所有邻居节点
    for (let node of nodes) {
      // 遍历当前节点的邻居节点
      if (result.includes(node)) continue; // 如果邻居节点已经在遍历结果中，则跳过
      result.push(node); // 将邻居节点添加到遍历结果中
      queue.push(node); // 将邻居节点添加到队列中，以便后续访问其邻居节点
    }
  }

  return result; // 返回遍历结果
}

console.log(bfs(graph, "B")); // 执行广度优先搜索，从起始节点 'B' 开始，并输出遍历结果

在上述代码中，图使用邻接表表示，bfs 函数使用队列实现了广度优先搜索。从起始节点 'A' 开始，将其加入队列并标记为已访问，然后依次从队列中取出节点，并访问其邻居节点，同时将邻居节点加入队列中，直到队列为空。

案例

深度优先搜索（DFS）和广度优先搜索（BFS）在前端项目中有许多实际的应用场景。下面有两个常见的前端开发项目案例

1、组件树遍历

在前端开发中，经常会有需要对组件树进行遍历的场景，例如渲染组件、查找组件等。下面是一个使用 DFS 进行组件树遍历的示例：

function dfs_component_traversal(component) {
  console.log(component); // 处理当前组件

  if (component.children) {
    for (const child of component.children) {
      dfs_component_traversal(child); // 递归遍历子组件
    }
  }
}

以上的代码展示了一个使用深度优先搜索进行组件树遍历的函数。我们可以根据组件的层级关系，从根组件开始递归地遍历每个组件及其子组件，以实现对整个组件树的遍历和操作。

这个算法可以帮助我们在前端项目中处理组件之间的关系，例如渲染组件、查找相关组件等。通过对组件树的深度遍历，我们可以有序地处理组件及其子组件，并执行相应的操作。

2、页面导航

在前端开发中，页面导航是一个常见的需求。我们可以使用广度优先搜索来实现页面导航功能，以确保按照层级关系有序地展示页面。

function bfs_page_navigation(page) {
  const queue = [page]; // 使用队列作为辅助数据结构来进行广度优先搜索

  while (queue.length > 0) {
    const current = queue.shift(); // 移除队列头部元素作为当前页面
    console.log(current); // 处理当前页面

    for (const child of current.children) {
      queue.push(child); // 将子页面加入队列
    }
  }
}

以上代码展示了一个使用广度优先搜索进行页面导航的函数。在这个函数中，我们使用队列作为辅助数据结构来进行广度优先搜索。通过不断将子页面加入队列，并按照队列中的顺序处理每个页面，可以实现按照层级关系有序地导航页面。

3、DFS + BFS 综合案例

const root = {
  value: 1,
  children: [
    {
      value: 2,
      children: [],
    },
    {
      value: 3,
      children: [
        {
          value: 7,
          children: [
            {
              value: 8,
              children: [],
            },
          ],
        },
      ],
    },
    {
      value: 4,
      children: [
        {
          value: 6,
          children: [],
        },
      ],
    },
  ],
};

// 在深度优先搜索 - 堆
// 我们首先处理当前节点，然后递归地处理每个子节点、直到叶子节点（没有子节点的节点），最后依次遍历完成
const digui = (node) => {
  console.log(node.value);
  if (node.children) {
    for (const children of node.children) {
      digui(children);
    }
  }
};
// 广度优先搜索-栈，把多维树结构，取出来平铺，依次访问。
// 在广度优先搜索中，我们使用队列来保存待访问的节点，确保按照层级顺序进行遍历。
// 每次从队列中取出队头节点，处理该节点后，将其邻居节点（子节点）入队，以便后续遍历。这样，就可以依次访问所有节点，并保持层级顺序。

function breadthFirstSearch(root) {
  if (!root) {
    return;
  }

  const queue = []; // 创建一个空队列，用于存放待访问的节点
  queue.push(root); // 将根节点入队

  while (queue.length !== 0) {
    // 当队列不为空时循环执行以下步骤
    const current = queue.shift(); // 出队队头节点作为当前节点
    console.log(current.value); // 进行二次加工或其他操作，这里简单地输出节点的值

    for (const child of current.children) {
      // 遍历当前节点的邻居节点（子节点）
      queue.push(child); // 将未访问过的邻居节点入队
    }
  }
}
console.log(digui(root));

console.log(breadthFirstSearch(root));

总结

递归函数本质上是一个在回调自身的函数，用于改造数据结构，重点在于跳出循环的机制，否则陷入死循环啦

深度优先搜索（DFS）的原理很简单：我们从起始节点开始，沿着一条路径不断向下探索，直到达到终点或者无法继续为止。如果遇到终点，就找到了一条路径；如果无法继续，则回溯到上一个节点，然后尝试探索其他路径。这个过程会递归地进行，或者使用栈来存储节点的顺序。

相比之下，广度优先搜索（BFS）的原理稍微有些不同：我们从起始节点开始，逐层地访问其邻居节点。也就是说，我们首先访问起始节点的邻居节点，然后是邻居节点的邻居节点，依此类推，直到遍历完所有节点或者找到目标节点为止。为了遍历节点的顺序，我们使用队列数据结构。

读者朋友好呀，我是王天~

尝试做过很多事情，汽修专业肄业生，半路出道的野生程序员、前端讲师、新手作者，最终还是喜欢写代码、乐于用文字记录热衷分享~

如文章有错误或者不严谨的地方，期待给于指正，万分感谢。

如果喜欢或者 有所启发，欢迎 star，对作者也是一种鼓励。

微信：「wangtian3111」，加我进王天唯一的读者群。

个人博客：https://itwangtian.com