PolarDB-X 2.0：使用一个透明的分布式数据库是一种什么体验

简介： 透明分布式，是PolarDB-X即将发布的能力，它能让应用在使用PolarDB-X的过程中，犹如使用单机数据库一般的体验。与传统的中间件类型的“分布式数据库”相比，有了透明分布式能力的PolarDB-X，不再需要应用考虑分区键的概念，应用可以完全将单机MySQL上开发的建表语句、应用代码直接迁移到PolarDB-X上运行起来。本文将为大家介绍PolarDB-X透明分布式的新体验。

透明分布式，是PolarDB-X即将发布的能力，它能让应用在使用PolarDB-X的过程中，犹如使用单机数据库一般的体验。

与传统的中间件类型的“分布式数据库”相比，有了透明分布式能力的PolarDB-X，不再需要应用考虑分区键的概念，应用可以完全将单机MySQL上开发的建表语句、应用代码直接迁移到PolarDB-X上运行起来。

本文将为大家介绍PolarDB-X透明分布式的新体验。

在PolarDB-X上安装一个WordPress

WordPress是一个开源的博客软件，它使用MySQL作为其数据库。操作是在PolarDB-X上安装一个WordPress，来体验PolarDB-X的透明分布式能力。

我们将遵循简单的三步走：

1. 不修改DDL直接建表
2. 不修改应用直接跑起来
3. 做下压测，做下调优

总结如下：

1. 使用官方的WordPress镜像，不做任何修改，其安装程序就能自动的在PolarDB-X上完成建表、数据初始化等工作，其使用的都是标准的MySQL语法。
2. 对此WordPress进行压测，PolarDB-X的各项监控数据显示，各节点处于的负载、数据量均处于均衡的状态。
3. 通过PolarDB-X提供的SQL分析、DAS等工具，可以方便的找到系统中热点SQL。
4. DBA可以直接通过创建索引、修改数据分布等DDL语句对系统性能做进一步的优化，不需要修改应用。

PolarDB-X实现透明分布式的武器

下面为大家分享下，PolarDB-X是如何实现透明分布式的。

透明数据分区

PolarDB-X是一个典型的Share Nothing的分布式数据库，其简化架构如下：

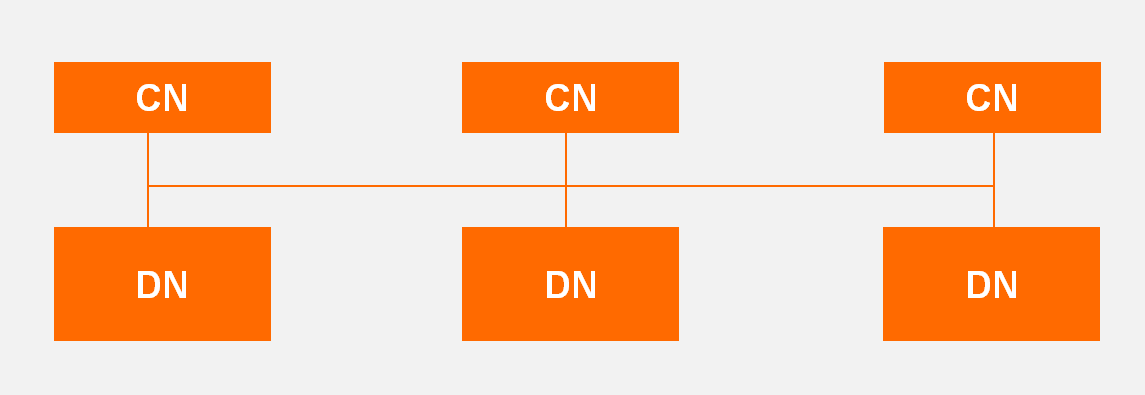
其核心组件为无状态的计算节点CN，与有状态的存储节点DN。

要了解PolarDB-X的透明分布式能力，首先要了解数据在PolarDB-X上是如何分布的。

在PolarDB-X中，一个表由多个索引组成，包括主键、二级索引等。PolarDB-X会对每个索引进行独立的进行分区，其分区键为索引的key。

例如一个典型的电商场景，订单表，拥有一个主键（id），两个索引（seller_id与buyer_id）：

create table orders (
   id bigint,
   buyer_id varchar comment '买家',
   seller_id varchar comment '卖家',
   primary key(id),
   index sdx(seller_id),
   index bdx(buyer_id)
)

• 对于主键索引，会按照id对其进行分区
• 对于索引sdx，会按照seller_id进行分区
• 对于索引bdx，会按照buyer_id进行分区

如下图所示：

对索引进行分片之后，PolarDB-X会将这些分片打散到不同的存储节点里，并会按照数据量等信息进行负载均衡，如下图所示：

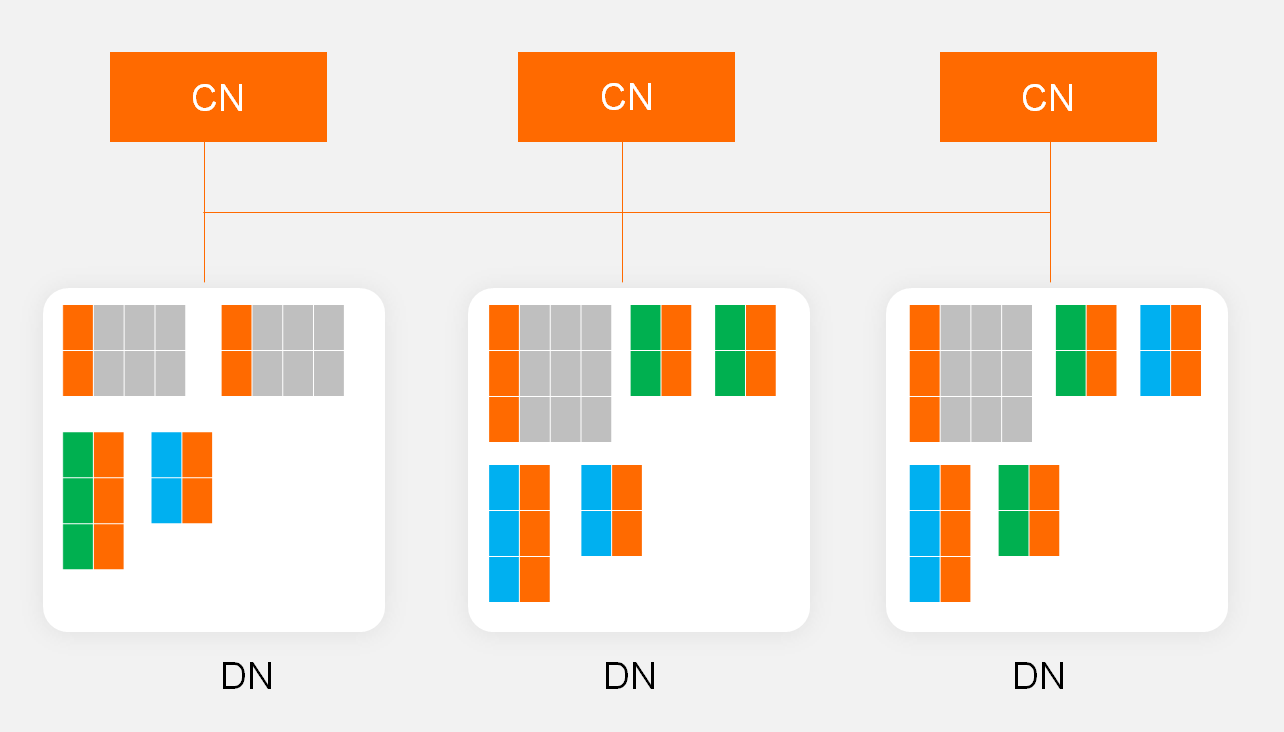
在PolarDB-X中，建表语句中可以不考虑分区键，PolarDB-X也能自动的对表进行分片与负载均衡。

因此，应用迁移PolarDB-X时，可以将单机MySQL中的建表语句导出，不需要修改直接在PolarDB-X中执行即可。

透明的分布式事务

分布式事务是PolarDB-X中的最重要的基础能力，它广泛的应用于业务内，避免了业务对事务代码进行改造；同时，PolarDB-X内部也用事务来实现索引。

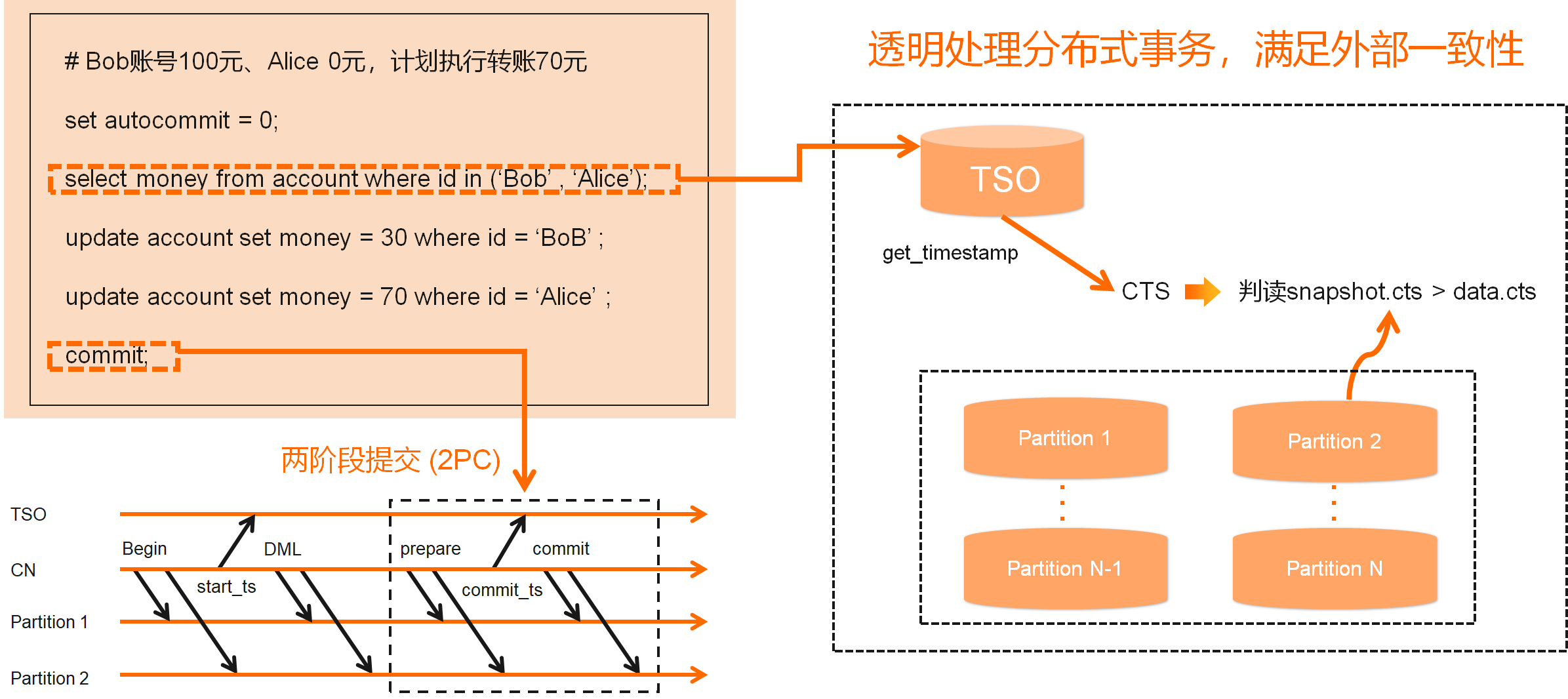
PolarDB-X的分布式事务有以下几个特征：

1. 与Spanner一样，满足外部一致性这种最强的一致性级别
2. 语法与MySQL完全兼容，无需对应用进行改造
3. 行为上支持兼容MySQL的RC与RR级别

Online DDL

PolarDB-X支持类型丰富的Online DDL，这里介绍一些有代表性的DDL类型。

索引维护

与单机MySQL的索引有所差异，PolarDB-X的索引均为全局索引，包含以下几种类型：

• 普通索引
• 唯一索引
• 聚簇索引

其中聚簇索引是PolarDB-X相对于MySQL的一种新类型的索引，它会包含表中的所有列，从而避免了回表的代价。

PolarDB-X中对索引的创建都通过DDL来完成，并且都是Online的，不会阻塞业务。

例如：

• 创建一个普通的索引：CREATE INDEX idx1 ON t1(name)
• 创建一个聚簇的索引：CREATE CLUSTERED INDEX idx1 ON t1(name)

INSTANT ADD COLUMN

加列操作是业务中最为常见的DDL类型。在MySQL中，加列操作的耗时是与数据量相关的（MySQL8.0中在表的最后面加列是INSTANT的）。

在PolarDB-X中，在任意位置加列都是INSTANT的，这个代表加列操作为恒定的秒级耗时，与数据量无关，不会对业务产生任何影响。

分区调整

PolarDB-X支持4种表的分布策略，Hash、Range、List、Broadcast。由于Hash能避免连续写入的热点，PolarDB-X默认使用Hash策略，大多数情况下，此策略能够很好的满足系统的性能需要。

但是如果业务在运行期间，希望选择合适的分区策略来提升系统性能，在PolarDB-X中可以方便的通过DDL语句进行调整，PolarDB-X会按照新的分区策略重新组织表的数据。

例如：

• 修改表的分区策略为Hash：ALTER TABLE t1 PARTITION BY HASH(name)
• 修改表的分片数为32：ALTER TABLE t1 PARTITION BY HASH(name) PARTITIONS 32
• 将表变为广播表：ALTER TABLE t1 BROADCAST
• 修改表的分区策略为RANGE：ALTER TABLE t1 PARTITION BY RANGE(id)

任意两种分区策略之间都可以通过DDL语句进行转换：

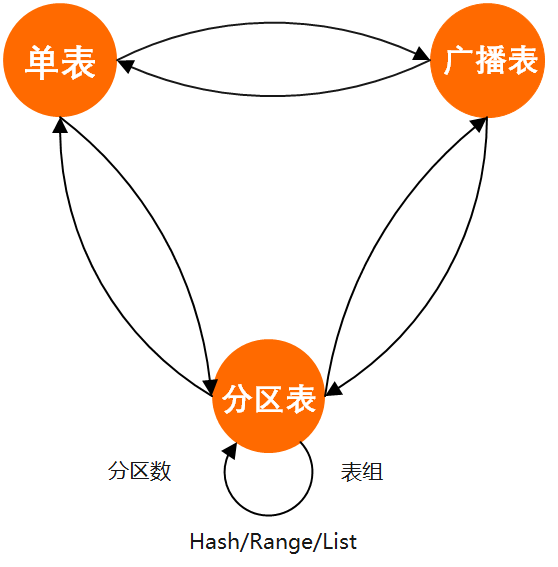
回填速度自适应

想必很多同学有过这样的经验：一个超大的表进行DDL操作，由于数据量比较大，这个DDL操作无法在一天内完成，为了避免对业务影响，人肉在白天业务高峰期来临的时候，调整参数，降低DDL的回填速度，晚上在业务高峰期结束后，提高DDL的回填速度。

PolarDB-X中的回填，会根据当前的系统负载，自动调节速度。

例如：

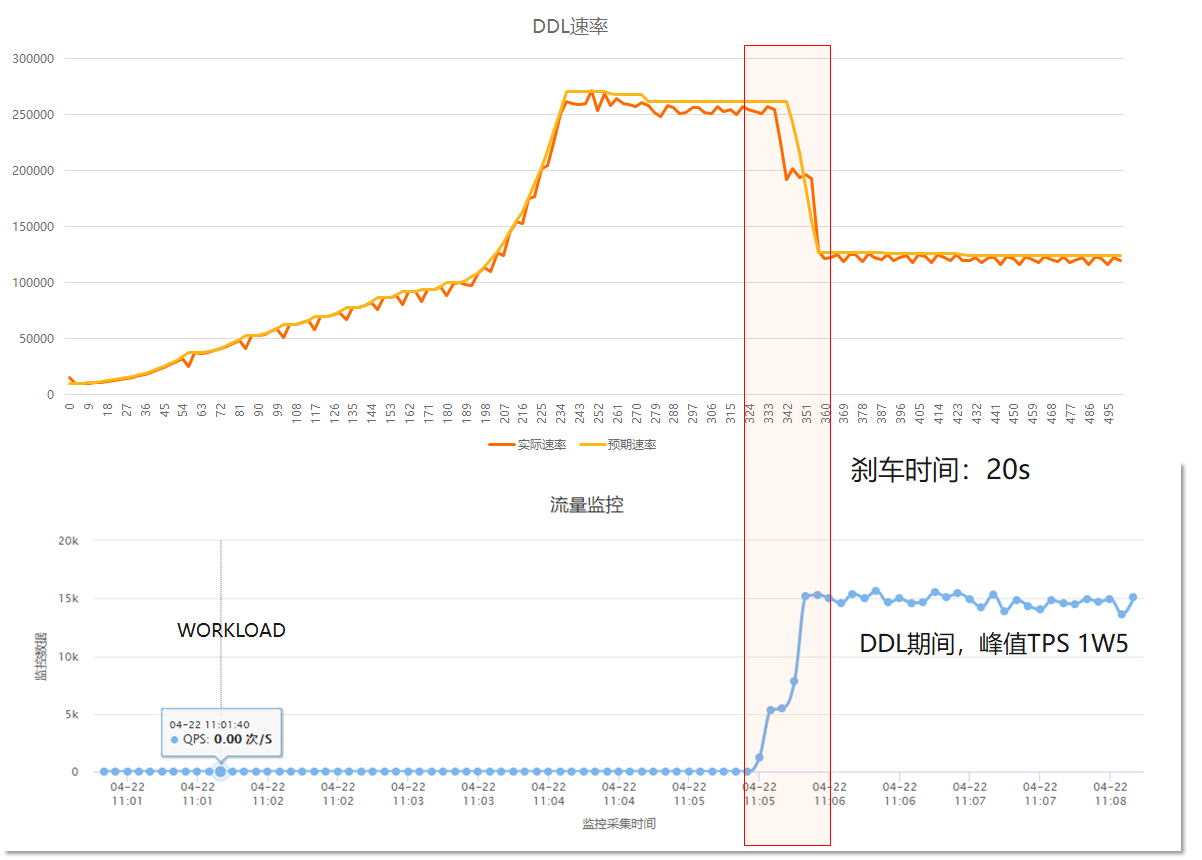
在这个例子中，分了四个阶段：

1. 开始没有业务负载，DDL回填速度上升到25W行/s
2. 业务负载开始上升，DDL回填速度迅速下降到13W行/s
3. 业务TPS稳定在1W5，DDL回填速度稳定在13W行/s
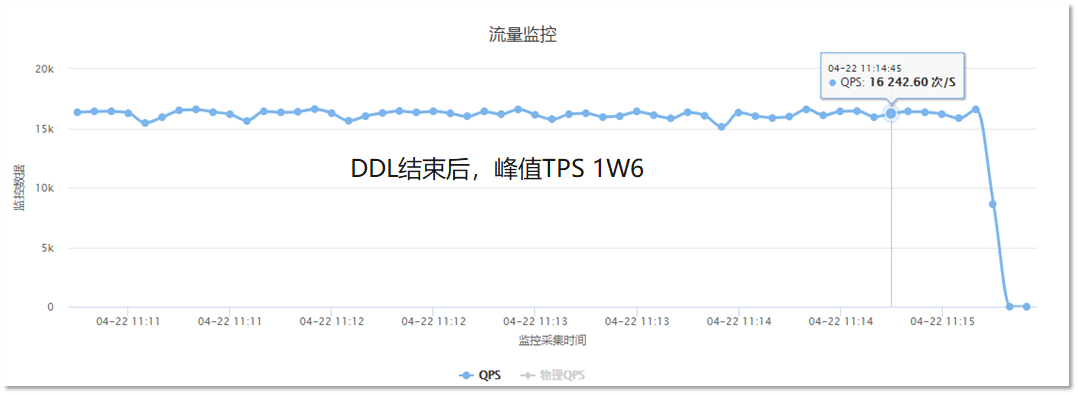
4. DDL结束后，业务TPS稳定在1W6

从这个例子中，我们可以看到PolarDB-X DDL的回填速度会自动根据业务负载进行调整，并且DDL期间，对业务的TPS影响很小。

让Online更Online

为了进一步减少DDL期间对业务的影响，PolarDB-X还使用了多项技术，例如：

• 元数据多版本，详见：https://zhuanlan.zhihu.com/p/347885003
• 可暂停、可取消
• MDL死锁检测

我们会在今后的文章里详细介绍这些技术的细节，请关注我们的知乎专栏：https://www.zhihu.com/org/polardb-x

总结

PolarDB-X的透明分布式能力，将极大的减少应用从单机数据库迁移分布式数据库的成本。同时，我们未来也会让它变得更透明，我们正在做的一些事情包括：

• 更精细的调度策略
• 热点数据的可视化展示，与SQL审计分析联动的智能诊断
• 在有全局索引的情况下，支持分区级的truncate
• 数据的按时间滚动、清理
• 等等

原文链接
本文为阿里云原创内容，未经允许不得转载。