动态规划二 & 贪心算法 实验三

一、贪心算法和动态规划法解决背包问题。

有一个背包其容积 C = 13。现有表格内的物品可以购买。

商品	价格 P	体积 V
啤酒	24	10
汽水	2	3
饼干	9	4
面包	10	5
牛奶	9	4

1 用动态规划法解决“0-1背包问题”

（1） 使用模块化开发的方式，把解决问题的过程抽象成三个模块，构造值结构的归并排序MergeSort类模块、处理值问题的背包Knapsack类模块和创建商品的KnapsackItem类模块。

（2） MergeSort类在Knapsack类中，被封装成处理归并排序的回调函数, 定义了最优值，负责在Knapsack类对sortPossibleItemsByWeight函数背包的weight由小到大进行排序，sortPossibleItemsByValue则对value由大到小执行排序，sortPossibleItemsByValuePerWeightRatio是price/weight的性价比，由大到小执行排序。其中Knapsack类又包含了处理购物清单selectedItems的totalValue()、totalWeight()、countCoin()、getLastProcduct()、setLastProcductValue(value)和setLastProcductWeight(weight)的功能函数，实现对购物清单里面的商品进行处理。 KnapsackItem类则实现了创建商品的对象，定义了商品的{value（价格）, weight（体积）, itemsInStock = 1（数量） ,produce（名称）}，实现对单个商品的totalValue()、totalWeight()、valuePerWeightRatio()、setValue(value)、setWeight(weight)和toString()进行商品属性处理的功能函数。

（3）0-1背包问题的solveZeroOneKnapsackProblem函数。

1)首先递归地对value降序排序，然后对weight进行升序排序，定义最优解的值。

2)再运用矩阵链乘法，创建一个子串长度与背包商品n和背包容积的n*m的空矩阵，第一维度的矩阵中每行的数据是用来定义对商品n的价格进行逐个比较的子串。第二维度的矩阵中每行列对应的数据是对每个物品从1至背包最大体积n的逐个价格的组合。从每一行中对价格的子问题进行累加记录，从而解决大问题，计算出最优的价格值。

3）最后通过循环遍历每件商品，用之前所得到最优的价格值矩阵，通过自底向上比较最后一行得到的最优值与上一行的最优值比较。如果两个值相同，则说明最后一行的物品没有被购买，不能选择价格最高者。如果两个值不相同，则说明当前商品被购买，应该加入购物清单。如此反复进行，最终构造购物清单的最优解。

2 核心函数实现代码。

solveZeroOneKnapsackProblem() {
    this.sortPossibleItemsByValue();
    this.sortPossibleItemsByWeight();
    this.selectedItems = [];
    const numberOfRows = this.possibleItems.length;
    const numberOfColumns = this.weightLimit;
    const knapsackMatrix = Array(numberOfRows).fill(null).map(() => {
      return Array(numberOfColumns + 1).fill(null);
    });
    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      knapsackMatrix[itemIndex][0] = 0;
    }
    for (let weightIndex = 1; weightIndex <= this.weightLimit; weightIndex += 1) {
      const itemIndex = 0;
      const itemWeight = this.possibleItems[itemIndex]._weight;
      const itemValue = this.possibleItems[itemIndex]._value;
      knapsackMatrix[itemIndex][weightIndex] = itemWeight <= weightIndex ? itemValue : 0;
    }
    for (let itemIndex = 1; itemIndex < this.possibleItems.length; itemIndex += 1) {
      for (let weightIndex = 1; weightIndex <= this.weightLimit; weightIndex += 1) {
        const currentItemWeight = this.possibleItems[itemIndex]._weight;
        const currentItemValue = this.possibleItems[itemIndex]._value;
        if (currentItemWeight > weightIndex) {
          knapsackMatrix[itemIndex][weightIndex] = knapsackMatrix[itemIndex - 1][weightIndex];
        } else {
          knapsackMatrix[itemIndex][weightIndex] = Math.max(
            currentItemValue + knapsackMatrix[itemIndex - 1][weightIndex - currentItemWeight],
            knapsackMatrix[itemIndex - 1][weightIndex],
          );
        }
      }
    }
    let itemIndex = this.possibleItems.length - 1;
    let weightIndex = this.weightLimit;
    while (itemIndex > 0) {
      const currentItem = this.possibleItems[itemIndex];
      const prevItem = this.possibleItems[itemIndex - 1];
      if (
        knapsackMatrix[itemIndex][weightIndex]
        && knapsackMatrix[itemIndex][weightIndex] === knapsackMatrix[itemIndex - 1][weightIndex]
      ) {
        const prevSumValue = knapsackMatrix[itemIndex - 1][weightIndex];
        const prevPrevSumValue = knapsackMatrix[itemIndex - 2][weightIndex];
        if (
          !prevSumValue
          || (prevSumValue && prevPrevSumValue !== prevSumValue)
        ) {
          this.selectedItems.push(prevItem);
        }
      } else if (knapsackMatrix[itemIndex - 1][weightIndex - currentItem._weight]) {
        this.selectedItems.push(prevItem);
        weightIndex -= currentItem._weight;
      }
      itemIndex -= 1;
    }
  }

3 背包内物品的组合与价格。

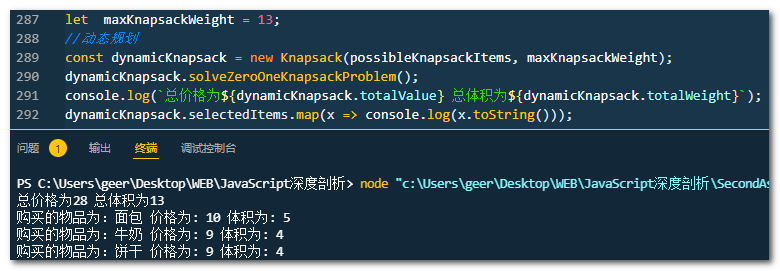
4 贪心算法解决“部分背包问题”的流程步骤。

贪心算法的前1-2步骤和动态规划相同，区别在于核心问题的处理函数。

部分背包问题的solveUnboundedKnapsackProblem函数。

1)首先递归地对value降序排序，然后通过price/weight性价比进行升序排序，定义最优解的值。

2）通过循环，每次选择性价比最高的商品。因为可以部分购买，只需由上往下，购买直至满足背包的最大体积。

5 核心函数实现代码。

solveUnboundedKnapsackProblem() {
    this.sortPossibleItemsByValue();
    this.sortPossibleItemsByValuePerWeightRatio();
    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      if (this.totalWeight < this.weightLimit) {
        const currentItem = this.possibleItems[itemIndex];
        const availableWeight = this.weightLimit - this.totalWeight;
 const maxPossibleItemsCount = Math.floor(availableWeight / currentItem._weight);
        if (maxPossibleItemsCount > currentItem.itemsInStock) {
          currentItem.quantity = currentItem.itemsInStock;
        } else if (maxPossibleItemsCount) {
          currentItem.quantity = maxPossibleItemsCount;
        }
        this.selectedItems.push(currentItem);
      }
    }
  }

6 背包内物品的组合与价格。

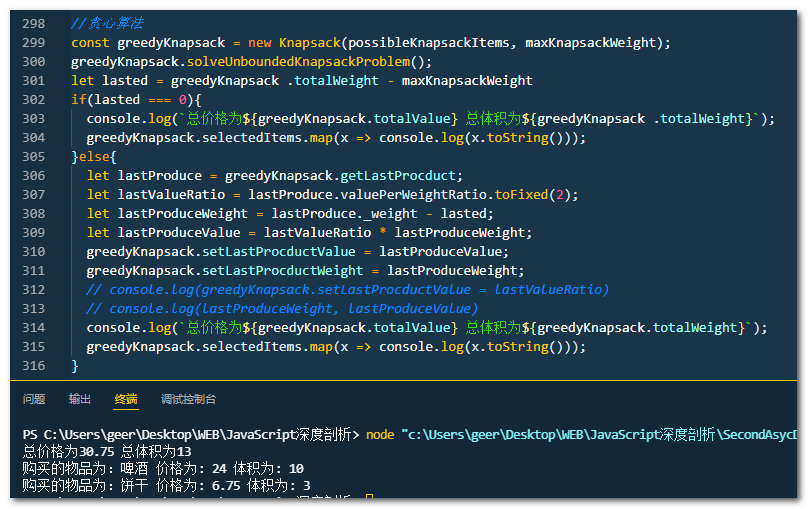
7 两种方法对于背包问题优点与缺点。

（1）动态规划：

优点：

1）可以获得商品价格每个组合的对比，得到全局最优解

2）动态规划方法反映了动态过程演变的联系和特征，在计算时可以利用实际知识和经验提高求解效率。

缺点：

1）空间需求大，需要额外的内存空间，并且一维问题可能需要二维空间。

2）构建解决问题的方法复杂，需要对寻找最优值进行大量处理。

（2）贪心算法：

优点：

1）空间和时间消耗相对比动态规划小

2）构建解决问题的方法简单，只需关注背包的体积

缺点：

1）不能保证求得的最后解是最佳的；

2）不能用来求最大或最小解问题；

3）只能求满足某些约束条件的可行解的范围。

二、 用贪心算法求解“找n分钱的最佳方案”

现在有面值分别为2角5分，1角，5分，1分的硬币，请给出找n分钱的最佳方案（要求找出的硬币数目最少）。

1 贪心算法解决“找n分钱的最佳方案”的流程步骤。

（1）基本定义和第一问动态规划定义1相同，把创建商品的KnapsackItem类换成CoinItem类模块。

（2） 基本定义和第一问动态规划定义2相同。
CoinItem类实现了创建商品的对象，定义了商品的{weight(n分钱), itemsInStock = 10000（存货数量）}，实现对单个商品的totalWeight()、setWeight(weight)、set quantity(quantity)和toString()进行硬币规格处理的功能函数。

（3）n分钱问题的solveCoinProblem函数。

1)首先使用sortCoinByWeight递归地对硬币规格降序排序，定义最优解的值。

2）由于硬币已大到小排序，由上往下，遍历n分钱。当this.possibleItems[itemIndex]._weight（当前硬币的规格） <= this.weightLimit（n分钱），通过maxPossibleItemsCount=Math.floor(availableWeight/currentItem._weight)求得凑齐n分钱每个规格的最大可能硬币个数。如果maxPossibleItemsCount
> currentItem.itemsInStock判断最大硬币个数超过定义的存货数量时，把当前存入的列表的硬币实际个数设置成硬币的存货数量，如果maxPossibleItemsCount && maxPossibleItemsCount > 0，判断硬币的最大可能数不能为负数或0，并把硬币实际个数设置最大可能硬币个数。最后如果该硬币的最大可能硬币个数为0，那么该硬币设置数量为0。

2 核心函数实现代码。

solveCoinProblem() {
    this.sortCoinByWeight()
    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      if (this.possibleItems[itemIndex]._weight <= this.weightLimit) {
        const currentItem = this.possibleItems[itemIndex];
        const availableWeight = this.weightLimit - this.totalWeight;
        const maxPossibleItemsCount = Math.floor(availableWeight / currentItem._weight);
        if (maxPossibleItemsCount > currentItem.itemsInStock) {
          currentItem._quantity = currentItem.itemsInStock;
        } else if (maxPossibleItemsCount && maxPossibleItemsCount > 0) {
          currentItem._quantity = maxPossibleItemsCount;
        }
        if(!maxPossibleItemsCount){
          currentItem._quantity = maxPossibleItemsCount;
        }
        this.selectedItems.push(currentItem);
      }
    }
  }

3 找5分钱、17分钱、22分钱、35分钱的最佳方案。

 完整代码：

class MergeSort{
    constructor(originalCallbacks) {
      this.callbacks = MergeSort.initSortingCallbacks(originalCallbacks);
      this.comparator = this.callbacks.compareCallback || MergeSort.defaultCompareFunction;
    }
    static initSortingCallbacks(originalCallbacks) {
      const callbacks = originalCallbacks || {};
      const stubCallback = () => {};

      callbacks.compareCallback = callbacks.compareCallback || undefined;
      callbacks.visitingCallback = callbacks.visitingCallback || stubCallback;

      return callbacks;
    }

    sort(originalArray) {
      if (originalArray.length <= 1) {
        return originalArray;
      }

      const middleIndex = Math.floor(originalArray.length / 2);
      const leftArray = originalArray.slice(0, middleIndex);
      const rightArray = originalArray.slice(middleIndex, originalArray.length);

      const leftSortedArray = this.sort(leftArray);
      const rightSortedArray = this.sort(rightArray);

      return this.mergeSortedArrays(leftSortedArray, rightSortedArray);
    }

    lessThan(a, b) {
      return this.comparator(a, b) < 0;
    }

    equal(a, b) {
      return this.comparator(a, b) === 0;
    }

    lessThanOrEqual(a, b) {
      return this.lessThan(a, b) || this.equal(a, b);
    }

    static defaultCompareFunction(a, b) {
      if (a === b) {
        return 0;
      }

      return a < b ? -1 : 1;
    }

    mergeSortedArrays(leftArray, rightArray) {
      const sortedArray = [];
      let leftIndex = 0;
      let rightIndex = 0;

      while (leftIndex < leftArray.length && rightIndex < rightArray.length) {
        let minElement = null;
        if (this.lessThanOrEqual(leftArray[leftIndex], rightArray[rightIndex])) {
          minElement = leftArray[leftIndex];
          leftIndex += 1;
        } else {
          minElement = rightArray[rightIndex];
          rightIndex += 1;
        }
        sortedArray.push(minElement);
      }

      return sortedArray
        .concat(leftArray.slice(leftIndex))
        .concat(rightArray.slice(rightIndex));
    }
}

const fp =  require('lodash/fp');
//背包
class Knapsack {

  constructor(possibleItems, weightLimit) {
    this.selectedItems = [];
    this.weightLimit = weightLimit;
    this.possibleItems = possibleItems;
  }

  sortPossibleItemsByWeight() {
    this.possibleItems = new MergeSort({

      compareCallback: (itemA, itemB) => {
        if (itemA._weight === itemB._weight) {
          return 0;
        }

        return itemA._weight < itemB._weight ? -1 : 1;
      },
    }).sort(this.possibleItems);
  }

  sortCoinByWeight() {
    this.possibleItems = new MergeSort({

      compareCallback: (itemA, itemB) => {
        if (itemA._weight === itemB._weight) {
          return 0;
        }

        return itemA._weight > itemB._weight ? -1 : 1;
      },
    }).sort(this.possibleItems);
  }

  sortPossibleItemsByValue() {
    this.possibleItems = new MergeSort({
      compareCallback: (itemA, itemB) => {
        if (itemA._value === itemB._value) {
          return 0;
        }

        return itemA._value > itemB._value ? -1 : 1;
      },
    }).sort(this.possibleItems);
  }

  sortPossibleItemsByValuePerWeightRatio() {
    this.possibleItems = new MergeSort({
      compareCallback: (itemA, itemB) => {
        if (itemA.valuePerWeightRatio === itemB.valuePerWeightRatio) {
          return 0;
        }

        return itemA.valuePerWeightRatio > itemB.valuePerWeightRatio ? -1 : 1;
      },
    }).sort(this.possibleItems);
  }

  solveZeroOneKnapsackProblem() {
    this.sortPossibleItemsByValue();
    this.sortPossibleItemsByWeight();
    this.selectedItems = [];
    // console.log(this.sortPossibleItemsByValue());
    // console.log(this.sortPossibleItemsByWeight());
    const numberOfRows = this.possibleItems.length;
    const numberOfColumns = this.weightLimit;
    console.log(numberOfRows, numberOfColumns)
    const knapsackMatrix = Array(numberOfRows).fill(null).map(() => {
      return Array(numberOfColumns + 1).fill(null);
    });
    // console.log(knapsackMatrix)

    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      knapsackMatrix[itemIndex][0] = 0;
    }
    for (let weightIndex = 1; weightIndex <= this.weightLimit; weightIndex += 1) {
      const itemIndex = 0;
      const itemWeight = this.possibleItems[itemIndex]._weight;
      const itemValue = this.possibleItems[itemIndex]._value;
      knapsackMatrix[itemIndex][weightIndex] = itemWeight <= weightIndex ? itemValue : 0;
    }

    for (let itemIndex = 1; itemIndex < this.possibleItems.length; itemIndex += 1) {
      for (let weightIndex = 1; weightIndex <= this.weightLimit; weightIndex += 1) {
        const currentItemWeight = this.possibleItems[itemIndex]._weight;
        const currentItemValue = this.possibleItems[itemIndex]._value;

        if (currentItemWeight > weightIndex) {
          knapsackMatrix[itemIndex][weightIndex] = knapsackMatrix[itemIndex - 1][weightIndex];
        } else {
          knapsackMatrix[itemIndex][weightIndex] = Math.max(
            currentItemValue + knapsackMatrix[itemIndex - 1][weightIndex - currentItemWeight],
            knapsackMatrix[itemIndex - 1][weightIndex],
          );
        }
      }
    }
    // console.log(knapsackMatrix)

    let itemIndex = this.possibleItems.length - 1;
    let weightIndex = this.weightLimit;
    while (itemIndex > 0) {
      const currentItem = this.possibleItems[itemIndex];
      const prevItem = this.possibleItems[itemIndex - 1];
      console.log('-----',currentItem,'---\n');
      if (
        knapsackMatrix[itemIndex][weightIndex]
        && knapsackMatrix[itemIndex][weightIndex] === knapsackMatrix[itemIndex - 1][weightIndex]
      ) {
        const prevSumValue = knapsackMatrix[itemIndex - 1][weightIndex];
        const prevPrevSumValue = knapsackMatrix[itemIndex - 2][weightIndex];
        if (
          !prevSumValue
          || (prevSumValue && prevPrevSumValue !== prevSumValue)
        ) {
          this.selectedItems.push(prevItem);
        }
      } else if (knapsackMatrix[itemIndex - 1][weightIndex - currentItem._weight]) {
        // console.log(currentItem._weight, currentItem.weight)
        this.selectedItems.push(prevItem);
        weightIndex -= currentItem._weight;
      }
      itemIndex -= 1;
    console.log(knapsackMatrix)
  }

  }

  solveUnboundedKnapsackProblem() {
    // this.sortPossibleItemsByValue();
    this.sortPossibleItemsByValuePerWeightRatio();
    console.log(this.possibleItems);
    // console.log(this.sortPossibleItemsByWeight());
    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      if (this.totalWeight < this.weightLimit) {
        const currentItem = this.possibleItems[itemIndex];

        const availableWeight = this.weightLimit - this.totalWeight;

        const maxPossibleItemsCount = Math.floor(availableWeight / currentItem._weight);

        if (maxPossibleItemsCount > currentItem.itemsInStock) {

          currentItem.quantity = currentItem.itemsInStock;
        } else if (maxPossibleItemsCount) {
          currentItem.quantity = maxPossibleItemsCount;
        }

        this.selectedItems.push(currentItem);
      }
    }
  }
  solveCoinProblem() {
    this.sortCoinByWeight()

    for (let itemIndex = 0; itemIndex < this.possibleItems.length; itemIndex += 1) {
      if (this.possibleItems[itemIndex]._weight <= this.weightLimit) {

        const currentItem = this.possibleItems[itemIndex];
        const availableWeight = this.weightLimit - this.totalWeight;
        const maxPossibleItemsCount = Math.floor(availableWeight / currentItem._weight);

        if (maxPossibleItemsCount > currentItem.itemsInStock) {
          currentItem._quantity = currentItem.itemsInStock;

        } else if (maxPossibleItemsCount && maxPossibleItemsCount > 0) {
          currentItem._quantity = maxPossibleItemsCount;
        }

        if(!maxPossibleItemsCount){
          currentItem._quantity = maxPossibleItemsCount;
        }

        this.selectedItems.push(currentItem);
      }
    }
  }
  get totalValue() {
    /** @var {KnapsackItem} item */
    return this.selectedItems.reduce((accumulator, item) => {
      return accumulator + item.totalValue;
    }, 0);
  }

  get totalWeight() {
    /** @var {KnapsackItem} item */
    return this.selectedItems.reduce((accumulator, item) => {
      return accumulator + item.totalWeight;
    }, 0);
  }
  get countCoin() {
    return this.selectedItems.reduce((accumulator, item) => {
      return accumulator + item._quantity;
    }, 0);
  }
  get getLastProcduct() {
    // console.log(fp.last(this.selectedItems));
    return fp.last(this.selectedItems);
  }
  set setLastProcductValue(value) {
    fp.last(this.selectedItems).value = value;
  }
  set setLastProcductWeight(weight) {
    fp.last(this.selectedItems).weight = weight
  }
}
class KnapsackItem {

  constructor({ value, weight, itemsInStock = 1 ,produce}) {
    // this.value = value;
    // this.weight = weight;
    this._value = value;
    this._weight = weight;
    this.itemsInStock = itemsInStock;
    this.produce = produce;
    this.quantity = 1;
  }

  get totalValue() {
    return this._value * this.quantity;
  }

  get totalWeight() {
    return this._weight * this.quantity;
  }

  get valuePerWeightRatio() {
    return this._value / this._weight;
  }
  set value(value) {
    this._value = value;
  }
  set weight(weight) {
    this._weight = weight;
  }
  toString() {

    return `购买的物品为：${this.produce} 价格为: ${this._value} 体积为: ${this._weight}`;
  }

}

class CoinItem {
  constructor({weight, itemsInStock = 1000}) {
    this._weight = weight;
    this.itemsInStock = itemsInStock;
    this._quantity = 1;
  }

  get totalWeight() {
    return this._weight * this._quantity;
  }

  set weight(weight) {
    this._weight = weight;
  }
  set quantity (quantity) {
    this._quantity = quantity;
  }
  toString() {
    return `币值为: ${this._weight} 数量为: ${this._quantity}`;
  }

}
const possibleKnapsackItems = [
  new KnapsackItem({produce: '啤酒', value: 24, weight: 10 }),//2.4
  new KnapsackItem({produce: '汽水', value: 2, weight: 3 }),//0.6
  new KnapsackItem({produce: '饼干', value: 9, weight: 4 }),//2.2
  new KnapsackItem({produce: '面包', value: 10, weight: 5 }),//2
  new KnapsackItem({produce: '牛奶', value: 9, weight: 4 }),//2.2
];

let  maxKnapsackWeight = 13;

//动态规划
const dynamicKnapsack = new Knapsack(possibleKnapsackItems, maxKnapsackWeight);
dynamicKnapsack.solveZeroOneKnapsackProblem();
console.log(`总价格为${dynamicKnapsack.totalValue} 总体积为${dynamicKnapsack.totalWeight}`);
dynamicKnapsack.selectedItems.map(x => console.log(x.toString()));
/*
*/
// maxKnapsackWeight = 13;
/*
//贪心算法
const greedyKnapsack = new Knapsack(possibleKnapsackItems, maxKnapsackWeight);
greedyKnapsack.solveUnboundedKnapsackProblem();
let lasted = greedyKnapsack .totalWeight - maxKnapsackWeight
if(lasted === 0){
  console.log(`总价格为${greedyKnapsack.totalValue} 总体积为${greedyKnapsack .totalWeight}`);
  greedyKnapsack.selectedItems.map(x => console.log(x.toString()));
}else{
  let lastProduce = greedyKnapsack.getLastProcduct;
  let lastValueRatio = lastProduce.valuePerWeightRatio.toFixed(2);
  let lastProduceWeight = lastProduce._weight - lasted;
  let lastProduceValue = lastValueRatio * lastProduceWeight;
  greedyKnapsack.setLastProcductValue = lastProduceValue;
  greedyKnapsack.setLastProcductWeight = lastProduceWeight;
  // console.log(greedyKnapsack.setLastProcductValue = lastValueRatio)
  // console.log(lastProduceWeight, lastProduceValue)
  console.log(`总价格为${greedyKnapsack.totalValue} 总体积为${greedyKnapsack.totalWeight}`);
  greedyKnapsack.selectedItems.map(x => console.log(x.toString()));
}
*/
/*
//贪心算法找硬币
const coin = [
  new CoinItem({ weight: 25 }),//2.4
  new CoinItem({ weight: 10 }),//0.6
  new CoinItem({ weight: 5 }),//2.2
  new CoinItem({ weight: 1 }),//2.2

];
let searchCoin = [5, 17, 22, 35];
searchCoin.map(x => {
  console.log('----------------------------------\n');
  console.log(`找 ${x} 分钱的最佳方案为：`)
  const greedyCoin = new Knapsack(coin, x);
  greedyCoin.solveCoinProblem();
  console.log(`总币值为${greedyCoin.totalWeight} 总硬币数目为 ${greedyCoin.countCoin}`);
  greedyCoin.selectedItems.filter(x => x._quantity > 0).map(x => console.log(x.toString()));
  console.log('\n----------------------------------');
});
*/
// console.log(greedyCoin.selectedItems);