图论(最短路&最小生成树)

图论

图的定义与概念

图的分类

图，根据点数和边数可分为三种：完全图，稠密图与稀疏图。

完全图，即\(m=n^2\)的图\((m\)为边数，\(n\)为点数\()\)。如：

1 1 0
1 2 1
1 3 2
2 1 1
2 2 0
2 3 3
3 1 2
3 2 3
3 3 0

这个数据是一个完全图。

稠密图，即\(m\)十分接近于\(n^2\)的图。如：

1 1 0
1 2 1
1 3 2
2 1 1
2 2 0
2 3 3
3 1 2

这个数据是一个稠密图。

稀疏图，即\(m\)远远低于\(n^2\)的图。如：

1 2 1
1 3 5
2 3 7
2 4 3
3 4 5

这个数据是一个稀疏图。

根据方向可分为两种：有向图和无向图。

有向图，就是边有方向，比如说，\(1\)_{$2$有一条边，而$2$}\(1\)没有边，则只能从\(1\)前往\(2\)，不能从\(2\)前往\(1\)，类似于现实中的单行道。

无向图，就是边无方向，比如说，\(1\)_{$2$有一条边，而$2$}\(1\)没有边，则可以从\(1\)前往\(2\)，也可以从\(2\)前往\(1\)，类似于现实中的双行道。

图的边权

就类似于现实中路的长度。

图大概长这样：

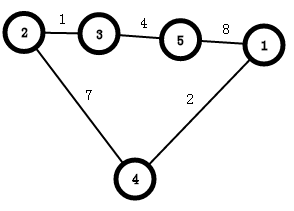
图的存储

邻接矩阵

适用于\(n \le 10000\)。

\(Code:\)

int dis[n][n];
int inf=99999999;
for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
    	if(i!=j)dis[i][j]=inf;
cin>>u>>v>>w;
dis[u][v]=w;

邻接矩阵，就是用矩阵来存储图，\(dis[i][j]\)即代表\(i\)~\(j\)的最短路径。如一个有向图：

1 1 0
1 2 1
1 3 2
2 1 1
2 2 0
2 3 3
3 1 2

这个数据用邻接表存储是这样的：

\(dis\)	\(1\)	\(2\)	\(3\)
\(1\)	0	1	2
\(2\)	1	0	3
\(3\)	2	inf	0

边表

适用于所有情况。

struct edge
{
	int u,v,w;
}e[m];
...
cin>>u>>v>>w;
e[cnt]={(edge)u,v,w};

邻接表

适用于所有情况。

int u[m],v[m],w[m],next[2*m],first[m];
...
cin>>u[cnt]>>v[cnt]>>w[cnt];
next[cnt]=first[u[cnt]];
first[u[cnt]]=cnt;

图的最短路

\(dijkstra(\)堆优化\()\)

时间复杂度：\(O((m+n)\) \(log\) \(n)\)

使用邻接表。

void dijkstra(int i)
{
	for(int j=0;j<=n;j++)
		dis[j]=inf;
	dis[i]=0;
	memset(book,false,sizeof(book));
	priority_queue<pair<int,int>>q;
	q.push(make_pair(0,i));
	while(q.size())
	{
		int x=q.top().second;
		q.pop();
		if(book[x])continue;
		book[x]=true;
		for(int k=first[x];k;k=next[k])
		{
			if(dis[v[k]]>dis[u[k]]+w[k])
			{
				dis[v[k]]=dis[u[k]]+w[k];
				q.push(make_pair(-dis[v[k]],v[k]));
			}
		}
	}
}

\(SPFA\)

时间复杂度：\(O(\)玄\()\)。

使用邻接表\(/\)边表。

void spfa(int i)
{
	for(int j=0;j<=n;j++)
		dis[j]=inf;
	dis[i]=0;
	memset(book,false,sizeof(book));
	queue<int>q;
	q.push(i);
	book[i]=true;
	while(!q.empty())
	{
		int k=first[q.front()];
		while(k!=-1)
		{
			if(dis[v[k]]>dis[u[k]]+w[k])
			{
				dis[v[k]]=dis[u[k]]+w[k];
				if(book[v[k]]==false)
				{
					q.push(v[k]);
					book[v[k]]=true;
				}
			}
			k=next[k];
		}
		book[q.front()]=false;
		q.pop();
	}
}

\(Floyd\)

时间复杂度：\(O(n^3)\)

使用邻接矩阵。

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)
    	for(int j=1;j<=n;j++)
        	dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

图的最小生成树

图的最小生成树指，权值和最小的生成树。

struct edge
{
	int u,v,w;
}e[3240010];
struct bcj
{
	int father[1810];
	void start(int n)
	{for(int i=0;i<=n;i++)father[i]=i;}
	int find(int x)
	{if(father[x]!=x)father[x]=find(father[x]);return father[x];}
	void unionn(int x,int y)
	{x=find(x);y=find(y);if(x!=y)father[y]=x;}
	bool judge(int x,int y)
	{if(find(x)==find(y))return true;return false;}
};
bool cmp(edge a,edge b)
{
	return a.w<b.w;
}
...
sort(e+1,e+1+m,cmp);
uf.start(n);
for(int i=1;i<=m;i++)
{
	if(!uf.judge(e[i].u,e[i].v))
    {
        cnt++;
        ans+=e[i].w;
        uf.unionn(e[i].u,e[i].v);
     }
     if(cnt==n-1)break;
}