SPFA全面讲解

——最短路高效算法

标签：最短路

简介：SPFA 是1994年在西安交通大学段凡丁同学所提出，是将Dijsktra以及Bellman-Ford两种最短路算法完美结合的一个算法，效率十分的高。全名为Shortest Path Faster Algorithm，简称SPFA。

首先，在下面的讲解中，我们要用到几个变量：

n 表示一共有n个点。
s 表示开始点。
t 表示结束点。
dist[MAXN]:d[i]表示从s到i的最短路径
head[MAXN]:head[i]记录前驱。
queue$<int>$q,也就是队列。
flag[MAXN]:f[i]表示i在不在队列中

$SPFA可以处理负权边!!$

首先add一个邻接表以及一个用来搞邻接表的struct

struct point
{
    int from;
    int to;
    int next;
    int len;
}edge[MAXN];
int total=0;
void add(int f,int t,int l)
{
    edge[total++].from=f;
    edge[total].to=t;
    edge[total].next=head[f];
    edge[total].len=l;
    head[f]=total;
}

首先，我们先处理初始化，顺带输入。。。

int main()
{
    scanf("%d%d",&n,&m);
    scanf("%d%d",&s,&t);
    for(int i=1;i<=n;i++)
    dist[i]=INF;
    //预处理操作
    {
        dist[s]=0;//源点到源点的距离为0
        q.push(s);//将源点入队
        flag[s]=1;//表示s点已经在队列中
    }
    SPFA(s);
}

然后就是队列+松弛操作。

int SPFA()
{
    while(!q.empty())
    {
        int cnt=q.front();
        q.pop();
        flag[cnt]=0;
        for(int i=head[cnt];i;i=edge[i].next)
            if(dist[edge[i].to]>dist[cnt]*edge[i].len)
            {
                dist[edge[i].to]=dist[cnt]*edge[i].len;
                if(!flag[edge[i].to])
                {
                    flag[flag[edge[i].to]]=1;
                    q.push(edge[i].to);
                }
            }
    }
}

那么正式的讲解从现在开始！！
首先我们建一个图用来方便讲解。

Title:现在我们建图, 里面包含有a b c d e f g
a->b: 24
a->d:15
a->c:8
c->f:3
c->e:7
f->e:2
b->e:6
e->g:9
g->b:3
f->g:3
f->d:5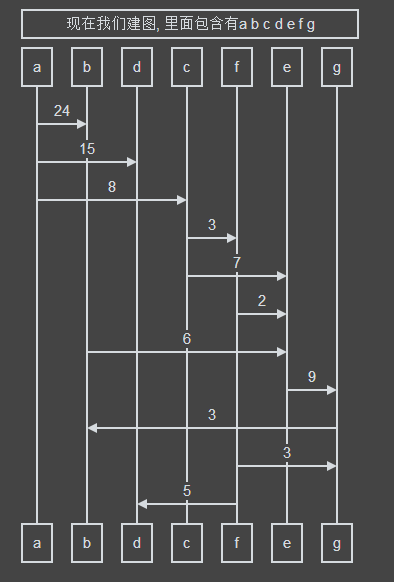

看不看得懂呢?~ ~ ~

然后我们假设a为s。
那么我们现在建立一个从起始点a到个点的最短路径表格。

a->a:0
a->b:&infin;
a->c:&infin;
a->d:&infin;
a->e:&infin;
a->f:&infin;
a->g:&infin;

然后按照我们的SPFA的顺序，首先a入队，然后判断到队列非空。
将队首元素a出队.

然后对以a点为起始点的所有边进行松弛操作（此处只有e点。）。

此时表格的状态为：

a->a:0
a->b:24
a->c:8
a->d:15
a->e:&infin;
a->f:&infin;
a->g:&infin;

在松弛的时候三个点的最短路径（估值）变小了，然后检测到这些点在队列中还都没有出现。于是入队，此时队列中有了三个点：b,c,d。
然后队首元素c出队.

对以c为起始点的所有边进行松弛操作。

此时表格的状态变为：

a->a:0
a->b:24
a->c:8
a->d:15
a->e:30
a->f:&infin;
a->g:&infin;

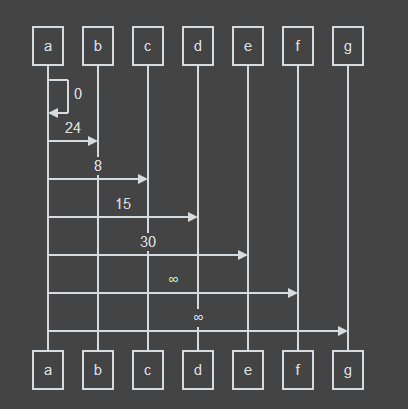
此时在列表中e的路径估值也变小了，而且e不在队列之中，于是e也入队，于是队列中的元素变成了c,d,e。
然后队首元素c再次出队.

对所有以c为起始点的边进行松弛操作。

此时表格又变了样子：

a->a:0
a->b:24
a->c:8
a->d:15
a->e:15
a->f:11
a->g:&infin;

看到了e和f的最短路径估值再次变小，但是e在队列中但是f不在，于是将f入队。
队首元素d出队

对以d为起始点的所有边进行松弛操作。

表格再次变化：

a->a:0
a->b:24
a->c:8
a->d:15
a->e:15
a->f:11
a->g:19

此时g的最短路径估值没有变小，于是松弛失败，没有新节点入队。于是接着取队首，f,g......
最后我们的表格变成了这个样子：

a->a:0
a->b:17
a->c:8
a->d:15
a->e:13
a->f:11
a->g:14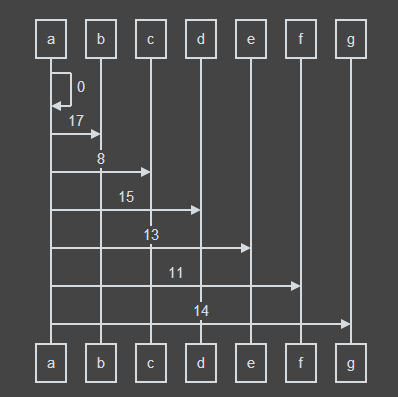

此时e的最短路径估值没有变化，于是松弛失败，此时队列为空，于是程序结束。
然后我们要求的dist[g]就是14。

$_完美收工_$ $_完美收工_$ $_完美收工_$ $_完美收工_$ $_完美收工_$ $_完美收工_$ $_完美收工_$

那么下面给大家出一道SPFA的模板题，（用来存代码（#滑稽）
若要看具体题面请看链接：传送门

##题目描述：最短路

给定n个带权的有向图，，求1到n的最短的简单路径之积。

输入：

一共m+1行。
第一行：两个数n,m.分别表示点的总数以及边的总数。
第2到第m+1行：每一行三个数：分别为两个点以及连接这两个点的边权。

输出：

一行，共一个数：表示所求路径的边权之积mod 9987的值。

输入样例：

3 3
1 2 3
2 3 3
1 3 10

输出样例：

很明显的模板题了。下面是代码：

//Yeasion_nein
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#define MAXN 10010
using namespace std;
int n,m,head[1000010];
int dist[1000010];
bool flag[1000010];
queue<int>q;
int total;
struct e
{
    int next;
    int to;
    int from;
    int len;
}edge[1000010];
void add(int f,int t,int l)
{
    edge[total++].from=f;
    edge[total].to=t;
    edge[total].next=head[f];
    edge[total].len=l;
    head[f]=total;
}
int SPFA()
{
    while(!q.empty())
    {
        int cnt=q.front();
        q.pop();
        flag[cnt]=0;
        for(int i=head[cnt];i;i=edge[i].next)
        {
            if(dist[edge[i].to]>dist[cnt]*edge[i].len)
            {
                dist[edge[i].to]=dist[cnt]*edge[i].len;
                if(!flag[edge[i].to])
                {
                    flag[flag[edge[i].to]]=1;
                    q.push(edge[i].to);
                }
            }
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    dist[i]=0x7ffffff;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d",&x);
        scanf("%d",&y);
        scanf("%d",&z);
        add(x,y,z);
    }
    dist[1]=1;
    q.push(1);
    flag[1]=1;
    SPFA();
    printf("%d",dist[n]%9987);
    return 0;
}

如果这篇博客有帮助到你的话，清点一下赞吧！！（qwq）