变分（图）自编码器不能直接应用于下游任务（GAE, VGAE, AE, VAE and SAE）

    自编码器是无监督学习领域中一个非常重要的工具。最近由于图神经网络的兴起，图自编码器得到了广泛的关注。笔者最近在做相关的工作，对科研工作中经常遇到的：自编码器（AE），变分自编码器（VAE），图自编码器（GAE）和图变分自编码器（VGAE）进行了总结。如有不对之处，请多多指正。

    另外，我必须要强调的一点是：很多文章在比较中将自编码器和变分自编码器视为一类，我个人认为，这二者的思想完全不同。自编码器的目的不是为了得到latent representation（中间层），而是为了生成新的样本。我自己的实验得出的结论是，变分自编码器和变分图自编码器生成的中间层不能直接用来做下游任务（聚类、分类等），这是一个坑。

自编码器（AE）

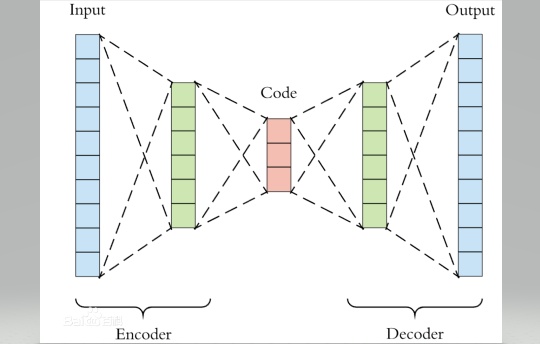
    在解释图自编码器之前，首先理解下什么是自编码器。自编码器的思路来源于传统的PCA，其目的可以理解为非线性降维。我们知道在传统的PCA中，学习器学得一个子空间矩阵，将原始数据投影到一个低维子空间，从未达到数据降维的目的。自编码器则是利用神经网络将数据逐层降维，每层神经网络之间得激活函数就起到了将"线性"转化为"非线性"的作用。自编码器的网络结构可以是对称的也可以是非对称的。我们下面以一个简单的四层对称的自编码器为例，全文代码见最后

   (严格的自编码器是只有一个隐藏层，但是我在这里把几种不同的自编码器统称为自编码器，其最大的区别就是隐藏层以及神经元数量的多少，理解一个，其它的都就理解了)

图自编码器（GAE）

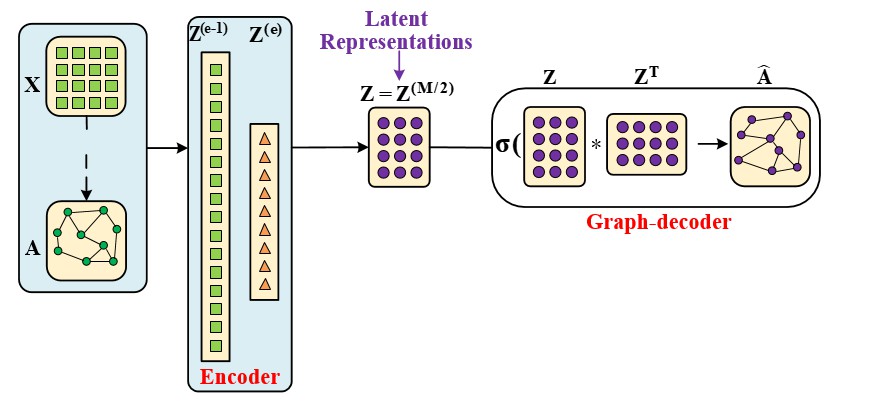
    图自编码器和自编码器最大的区别有两点：一是图自编码器在encoder过程中使用了一个（n*n）的卷积核；另一个是图编码器没有数据解码部分，转而代之的是图decoder。

图自编码器可以像自编码器那样用来生成隐向量，也可以用来做链路预测（类似于推荐任务）。

变分自编码器（VAE）

   变分自编码是让中间层Z服从一个分布。这样我们想要生成一个新的样本的时候，就可以直接在特定分布中随机抽取一个样本。

   另外，我初学时遇到的疑惑，就是中间层是怎么符合分布的。我的理解是：

      输入样本：\(\mathbf{X \in \mathcal{R}^{n * d}}\)

      中间层 ：\(\mathbf{Z \in \mathcal{R}^{n * m}}\)

   所谓的正态分布是让\(Z\)的每一行\(z_i\)符合正态分布，这样才能随机从正态分布中抽一个新的\(z_i\)出来。但是正是这个原因，我认为\(Z\)不能直接用来处理下游任务（分类、聚类）,我自己跑实验确实效果不好。

变分图自编码器（VGAE）

    如果你理解了变分比编码器和图自编码器，那么变分图自编码器你也就能理解了。第一个改动就是在VAE的基础上把encoder过程换成了GCN的卷积过程，另一个改动就是把decoder过程换成了图decoder过程。同样生成的中间层隐向量不能直接应用下游任务。

   数据集和下游任务的代码见: https://github.com/zyx423/GAE-and-VGAE.git

全文代码如下：

class myAE(torch.nn.Module):

    def __init__(self, d_0, d_1, d_2, d_3, d_4):
        super(myAE, self).__init__()
        // 这里的d0, d_1, d_2, d_3, d_4对应四层神经网络的维度

        self.conv1 = torch.nn.Sequential(
            torch.nn.Linear(d_0, d_1, bias=False),
            torch.nn.ReLU(inplace=True)
        )

        self.conv2 = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False),
            torch.nn.ReLU(inplace=True)
        )

        self.conv3 = torch.nn.Sequential(
            torch.nn.Linear(d_2, d_3, bias=False),
            torch.nn.ReLU(inplace=True)
        )

        self.conv4 = torch.nn.Sequential(
            torch.nn.Linear(d_3, d_4, bias=False),
            torch.nn.Sigmoid()
        )
    def Encoder(self, H_0):
        H_1 = self.conv1(H_0)
        H_2 = self.conv2(H_1)
        return H_2

    def Decoder(self, H_2):
        H_3 = self.conv3(H_2)
        H_4 = self.conv4(H_3)
        return H_4

    def forward(self, H_0):
        Latent_Representation = self.Encoder(H_0)
        Features_Reconstrction = self.Decoder(Latent_Representation)
        return Latent_Representation, Features_Reconstrction

class myGAE(torch.nn.Module):
    def __init__(self, d_0, d_1, d_2):
        super(myGAE, self).__init__()

        self.gconv1 = torch.nn.Sequential(
            torch.nn.Linear(d_0, d_1, bias=False),
            torch.nn.ReLU(inplace=True)
        )
        self.gconv1[0].weight.data = get_weight_initial(d_1, d_0)

        self.gconv2 = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False)
        )
        self.gconv2[0].weight.data = get_weight_initial(d_2, d_1)

    def Encoder(self, Adjacency_Modified, H_0):
        H_1 = self.gconv1(torch.matmul(Adjacency_Modified, H_0))
        H_2 = self.gconv2(torch.matmul(Adjacency_Modified, H_1))
        return H_2

    def Graph_Decoder(self, H_2):
        graph_re = Graph_Construction(H_2)
        Graph_Reconstruction = graph_re.Middle()
        return Graph_Reconstruction

    def forward(self, Adjacency_Modified, H_0):
        Latent_Representation = self.Encoder(Adjacency_Modified, H_0)
        Graph_Reconstruction = self.Graph_Decoder(Latent_Representation)
        return Graph_Reconstruction, Latent_Representation

class myVAE(torch.nn.Module):
    def __init__(self, d_0, d_1, d_2, d_3, d_4, bias=False):
        super(myVAE, self).__init__()

        self.conv1 = torch.nn.Sequential\
        (
            torch.nn.Linear(d_0, d_1, bias= False),
            torch.nn.ReLU(inplace=True)
        )

        # VAE有两个encoder，一个用来学均值，一个用来学方差
        self.conv2_mean = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False)

        )
        self.conv2_std = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False)
        )
        self.conv3 = torch.nn.Sequential(
            torch.nn.Linear(d_2, d_3, bias=False),
            torch.nn.ReLU(inplace=False)
        )
        self.conv4 = torch.nn.Sequential(
            torch.nn.Linear(d_3, d_4, bias=False),
            torch.nn.Sigmoid()
        )

    def Encoder(self, H_0):
        H_1 = self.conv1(H_0)
        H_2_mean = self.conv2_mean(H_1)
        H_2_std = self.conv2_std(H_1)
        return H_2_mean, H_2_std

    def Reparametrization(self, H_2_mean, H_2_std):
        # sigma = 0.5*exp(log(sigma^2))= 0.5*exp(log(var))
        std = 0.5 * torch.exp(H_2_std)
        # N(mu, std^2) = N(0, 1) * std + mu。
        # 数理统计中的正态分布方差，刚学过， std是方差。
        # torch.randn 生成正态分布
        Latent_Representation = torch.randn(std.size()) * std + H_2_mean
        return Latent_Representation

    # 解码隐变量
    def Decoder(self, Latent_Representation):
        H_3 = self.conv3(Latent_Representation)
        Features_Reconstruction = self.conv4(H_3)
        return Features_Reconstruction

    # 计算重构值和隐变量z的分布参数
    def forward(self, H_0):
        H_2_mean, H_2_std = self.Encoder(H_0)
        Latent_Representation = self.Reparametrization(H_2_mean, H_2_std)
        Features_Reconstruction = self.Decoder(Latent_Representation)
        return Latent_Representation, Features_Reconstruction, H_2_mean, H_2_std

class myVGAE(torch.nn.Module):
    def __init__(self, d_0, d_1, d_2):
        super(myVGAE, self).__init__()

        self.gconv1 = torch.nn.Sequential(
            torch.nn.Linear(d_0, d_1, bias=False),
            torch.nn.ReLU(inplace=True)
        )
        # self.gconv1[0].weight.data = get_weight_initial(d_1, d_0)

        self.gconv2_mean = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False)
        )
        # self.gconv2_mean[0].weight.data = get_weight_initial(d_2, d_1)

        self.gconv2_std = torch.nn.Sequential(
            torch.nn.Linear(d_1, d_2, bias=False)
        )
        # self.gconv2_std[0].weight.data = get_weight_initial(d_2, d_1)

    def Encoder(self, Adjacency_Modified, H_0):
        H_1 = self.gconv1(torch.matmul(Adjacency_Modified, H_0))
        H_2_mean = self.gconv2_mean(torch.matmul(Adjacency_Modified, H_1))
        H_2_std = self.gconv2_std(torch.matmul(Adjacency_Modified, H_1))
        return H_2_mean, H_2_std

    def Reparametrization(self, H_2_mean, H_2_std):

        # sigma = 0.5*exp(log(sigma^2))= 0.5*exp(log(var))
        std = 0.5 * torch.exp(H_2_std)
        # N(mu, std^2) = N(0, 1) * std + mu。
        # 数理统计中的正态分布方差，刚学过， std是方差。
        # torch.randn 生成正态分布
        Latent_Representation = torch.randn(std.size()) * std + H_2_mean
        return Latent_Representation

    # 解码隐变量
    def Graph_Decoder(self, Latent_Representation):
        graph_re = Graph_Construction(Latent_Representation)
        Graph_Reconstruction = graph_re.Middle()
        return Graph_Reconstruction

    def forward(self, Adjacency_Modified, H_0):
        H_2_mean, H_2_std = self.Encoder(Adjacency_Modified, H_0)
        Latent_Representation = self.Reparametrization(H_2_mean, H_2_std)
        Graph_Reconstruction = self.Graph_Decoder(Latent_Representation)
        return Latent_Representation, Graph_Reconstruction, H_2_mean, H_2_std