[Computer Vision]Harris角点检测的详细推导

Harris角点检测

思想

为什么要检测角点呢？因为角点的特征比较明显。进行角点检测的朴素思想是利用图像梯度，也就是根据图像强度的变化来寻找角点。如图所示

这里举了个例子，给定一个小的区域（Patch），当这个小区域在不同位置滑动的时候，所呈现出来的一些特性是不同的，根据图示，有三个方面。

• Flat，平的地方，在任何方向，梯度都没什么变化。
• Edge，边的地方，当沿着边方向的时候，梯度没什么变化。
• Corner，角的地方，沿着任何方向，梯度都有变化。

Error Function

\[E(u,v)=\sum_{x,y}{w(x,y)[I(x+u,y+v)-I(x,y)]^2}
\]

• \(x,y\)是相对于一个小patch来说的，例如一个5*5的区域
• \((u,v)\)是一个很小的移动量
• \(w(x,y)\)是windows function，也就是对于每个点的权重，例如想让中心的点权重高，可以用高斯核，一般就是全1或者高斯。
• \(I(x,y)\)就代表图像在\((x,y)\)的强度值。
• 后面做差其实就是类似求梯度一样

根据之前的讨论，在一个patch里，如果有角点的存在，各个方向的梯度值都很大，于是乎，我们的目标是让\(E(u,v)\)尽可能的大。

因为\((u,v)\)的值很小，所以我们可以利用二元函数的泰勒展开，来近似计算。

二元函数的泰勒展开，当然扔掉了一些项。

\[f(x+u,y+v) \approx f(x,y)+uf_x(x,y)+vf_y(x,y)
\]

那么我们对Error function中的关键部分进行展开

\[\begin{aligned}
[I(x+u,y+v)-I(x,y)]^2 &\approx [I(x,y)+uI_x+vI_y-I(x,y)]\\
&=(uI_x+vI_y)^2\\
&=[u,v]
\begin{bmatrix}
I_x^2 &I_xI_y\\
I_xI_y&I_y^2
\end{bmatrix}
\begin{bmatrix}
u\\v
\end{bmatrix}
\end{aligned}
\]

所以Error Function可以近似为

\[E(u,v)\approx [u,v]M\begin{bmatrix}
u\\v
\end{bmatrix}
\]

\[M=
\sum_{x,y}{w(x,y)
\begin{bmatrix}
I_x^2 &I_xI_y\\
I_xI_y&I_y^2
\end{bmatrix}
}
\]

这就涉及到线性代数里的二次型问题了。

简单的二次型

例如 \(f(x,y) = x^2+y^2\)的可以写作矩阵的形式

\[[x,y]\begin{bmatrix}
1 & 0\\
0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\y
\end{bmatrix}
\]

由中间这个矩阵来决定这个二次型的形状，因为我们研究的二次型只有两个变量，所以可以可视化来理解如下图所示。对形状矩阵可以进行特征分解，分为中间的对角阵（对角线都是特征值）两边是特征向量。特征向量代表了椭圆切片的长短轴的方向，而特征值平方根的倒数代表了轴的长短。至于为什么分解完会和椭圆对应，线性代数书上会有。

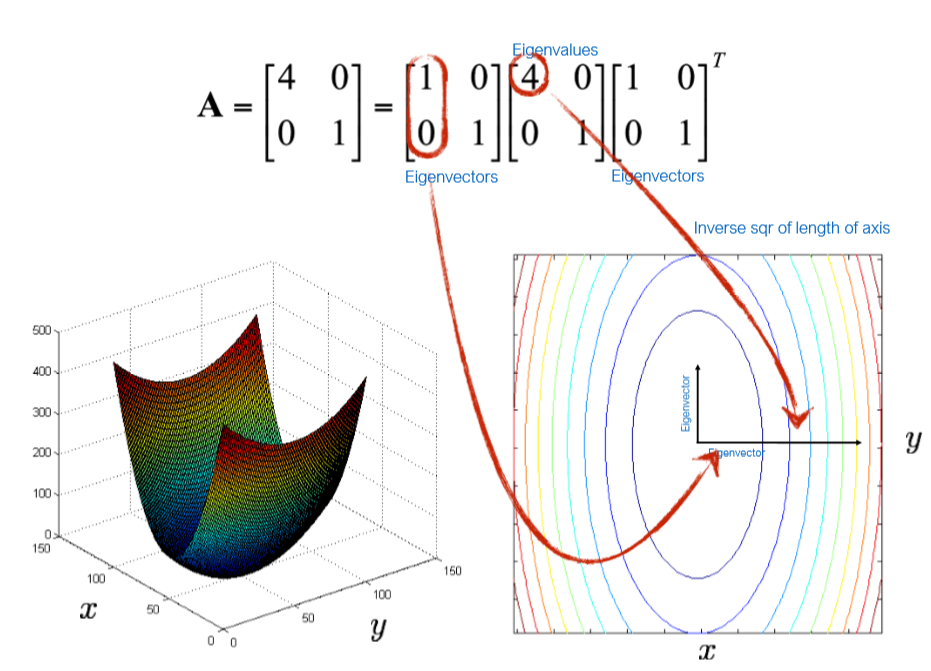
这样就把Error Function给可视化了，有了几何含义，更加直观了。

• Flat的时候，\((u,v)\)往哪个方向变化都不大，反应在几何上，应该是一个较为平坦的面
• Edge的时候，\((u,v)\)往某个方向变化大，反应在几何上，应该是某个方向翘起。
• Corner的时候，\((u,v)\)往大部分方向变化都大，反应在几何上，应该是大部分方向都翘起。

如图所示

我们可以通过两个特征值之间的大小关系，以及他们自身的关系来作为评估的依据。

当两个特征值都很大，且差不多时，意味着角点。

角点响应的度量

以上分析了，要两个特征值都很大，且同时大，那怎么来度量？于是乎在最原始的论文里，这样定义了响应函数，并且对不同的\(\lambda\)有以下的响应图

\[R = det(M)-k(trace(M))^2\\
det(M) = \lambda_1\lambda_2\\
trace(M) = \lambda_1+\lambda_2
\]

\(k\)一般在是0.04-0.06

如图所示，黄色的线是等值线，代表\(R\)的值都相同，左上角是\((0,0)\)点，往右下角去\(R\)的值越大，代表角点的响应越高，图中画了个绿线，右侧的R值基本可以判断为是角点了。另外还有一些别的响应函数，基本大同小异吧。

算法

所以现在经过以上的分析，总结一下角点检测的算法步骤。

1. 计算整个图像的梯度值\(I_x,I_y\)
2. 对于每个像素的\(I_{x^2}=I_xI_x,I_{y^2}=I_yI_y,I_{xy}=I_xI_y\)
3. 计算每一个像素窗口的和，意思就是对于一个像素，定义一个领域例如5*5，就和之前提及的那样，然后计算这个邻域里面所有第二步计算出来的值的和。\(S_{x^2}=G_{\sigma}*I_{x^2},S_{y^2}=G_{\sigma}*I_{y^2},S_{xy}=G_{\sigma}*I_{xy}\)
4. 对于每个点\((x,y)\)，定义矩阵\(\begin{bmatrix}S_{x^2}&S_{xy}\\S_{xy}&S_{y^2}\end{bmatrix}\)
5. 对于每个点，计算响应值\(R=Det(H)-k(Trace(H))^2\)
6. 对\(R\)设定阈值，并且计算非极大值抑制（nonmax suppression, NMS），这个的意思应该就是比如5*5的邻域内有好几个点通过了阈值的筛选，那么选择最大的那个，抑制其他的点。

一些特性

• Harris角点响应具有旋转不变性，因为旋转不会改变特征值的大小。
• Harris角点响应对强度变化具有一定的不变性，缩放或者平移。因为经过缩放或者平移，最大值还是最大值，但是阈值可能要改改。
• Harris角点响应不对尺度有不变性，改变尺度可能会改变检测的结果。可能在某一尺度下检测出为角点，而另一尺度检测出为边缘。

参考

• [1]CSE486 PSU http://www.cse.psu.edu/~rtc12/CSE486/
• [2]16-385 CMU 5http://www.cs.cmu.edu/~16385/