P4147 玉蟾宫 题解

CSDN同步

原题链接

简要题意：

求最大 \(0\) 矩阵。（将字符转化为数字）

本题是模板题，可以用来爆踩。？？？

悬线法 来了！

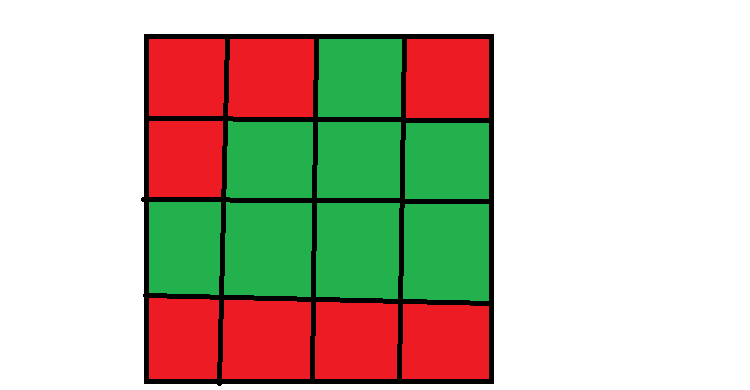
其中绿色是 \(0\)，红色是 \(1\).

下面以这个图为例讲一下算法流程。

我们首先求出，以每个格子为最下面，往上堆积的最长的 \(0\) 条。

则所有格子的值为：

0 0 1 0
0 1 2 1
1 2 3 2
0 0 0 0

下面，对每一行，求以这一行为底的最大矩阵。

第一行：只能以 \(a_{1,3}\) 为底，无法往左右扩展，此时答案为 \(1 \times (3-3+1) = 1\).

第二行：对于 \(a_{2,2}\)，可以往左扩展至 \(2,2\)，往右扩展至 \(2,4\)，此时答案为 \(1 \times (4-2+1) = 3\).

而 \(a_{4,2}\) 同理。

但 \(a_{3,3}\) 往上可以扩展 \(1\) 格，左右不得扩展，因此答案为 \(2 \times (3-3+1) = 2\).

所以整个第二行的答案为 \(\max(3,2,3) = 3\).

第三行：

对于 \(a_{3,1}\) ，左右扩展 \(4\) 格，往上只有 \(1\) 格，答案为 \(4\).

对于 \(a_{3,2}\) ，左右扩展 \(3\) 格，往上只有 \(2\) 格，答案为 \(6\).

而 \(a_{3,3}\) ，\(a_{4,4}\) 同。

所以第三行的答案为 \(\max(4,6,6,6) = 6\).

第四行没有绿格，所以答案为 \(0\).

综上，答案为 \(\max(1,3,6,0) = 6\).

大家应该都懂了吧！

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;

const int N=1e3+1;

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

int n,m,a[N][N],h[N][N];
int l[N][N],r[N][N],ans=0;

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++) {
		char c; cin>>c;
		a[i][j]=(c=='F')?0:1;
//		l[i][j]=r[i][j]=j; h[i][j]=1;
	} for(int j=1;j<=m;j++) r[0][j]=m+1;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) h[i][j]=(!a[i][j])?(h[i-1][j]+1):0; //往上扩展
		int t=0;
		for(int j=1;j<=m;j++)
			if(!a[i][j]) l[i][j]=max(l[i-1][j],t);
			else l[i][j]=0,t=j; //往左扩展
		t=m+1; for(int j=m;j;j--)
			if(!a[i][j]) r[i][j]=min(r[i-1][j],t);
			else r[i][j]=m+1,t=j; //往右扩展
		for(int j=1;j<=m;j++) ans=max(ans,(r[i][j]-l[i][j]-1)*h[i][j]);
	} printf("%d\n",ans*3); //别忘了*3
	return 0;
}