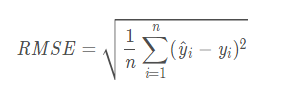MSE(均方误差)、RMSE (均方根误差)、MAE (平均绝对误差)
1、MSE(均方误差)(Mean Square Error)
MSE是真实值与预测值的差值的平方然后求和平均。
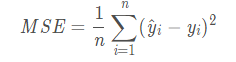
范围[0,+∞),当预测值与真实值完全相同时为0,误差越大,该值越大。
import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
2、
RMSE (均方根误差)(Root Mean Square Error)
import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
3、MAE (平均绝对误差)(Mean Absolute Error)

import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
print(metrics.mean_absolute_error(y_true, y_pred))
MSE(均方误差)、RMSE (均方根误差)、MAE (平均绝对误差)的更多相关文章
- 回归评价指标MSE、RMSE、MAE、R-Squared
分类问题的评价指标是准确率,那么回归算法的评价指标就是MSE,RMSE,MAE.R-Squared. MSE和MAE适用于误差相对明显的时候,大的误差也有比较高的权重,RMSE则是针对误差不是很明显的 ...
- 机器学习:衡量线性回归法的指标(MSE、RMSE、MAE、R Squared)
一.MSE.RMSE.MAE 思路:测试数据集中的点,距离模型的平均距离越小,该模型越精确 # 注:使用平均距离,而不是所有测试样本的距离和,因为距离和受样本数量的影响 1)公式: MSE:均方误差 ...
- 均方根误差(RMSE)与平均绝对误差(MAE)
RMSE Root Mean Square Error,均方根误差 是观测值与真值偏差的平方和与观测次数m比值的平方根. 是用来衡量观测值同真值之间的偏差 MAE Mean Absolute Erro ...
- 均方根误差(RMSE),平均绝对误差 (MAE),标准差 (Standard Deviation)
来源:https://blog.csdn.net/capecape/article/details/78623897 RMSE Root Mean Square Error, 均方根误差是观测值与真值 ...
- 机器学习入门-随机森林温度预测-增加样本数据 1.sns.pairplot(画出两个关系的散点图) 2.MAE(平均绝对误差) 3.MAPE(准确率指标)
在上一个博客中,我们构建了随机森林温度预测的基础模型,并且研究了特征重要性. 在这个博客中,我们将从两方面来研究数据对预测结果的影响 第一方面:特征不变,只增加样本的数据 第二方面:增加特征数,增加样 ...
- 第3章 衡量线性回归的指标:MSE,RMSE,MAE
, , ,, , , ,
- 学习笔记54—均方误差(MSE)和均方根误差(RMSE)和平均绝对误差(MAE)
https://blog.csdn.net/reallocing1/article/details/56292877 MSE: Mean Squared Error 均方误差是指参数估计值与参数真值 ...
- 方差(variance)、标准差(Standard Deviation)、均方差、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)
方差(variance).标准差(Standard Deviation).均方差.均方根值(RMS).均方误差(MSE).均方根误差(RMSE) 2017年10月08日 11:18:54 cqfdcw ...
- 回归模型效果评估系列2-MAE、MSE、RMSE、MAPE(MAPD)
MAE.MSE.RMSE.MAPE(MAPD)这些都是常见的回归预测评估指标,重温下它们的定义和区别以及优缺点吧 MAE(Mean Absolute Error) 平均绝对误差 ...
随机推荐
- 002. 使用IDEA创建MyBatis的JAVAWEB项目 ,每一步都有详细过程,完美绕过各种坑能正常运行
001. 我们新建一个Module,相当于一个工程里面的一个项目 002.选择空白的JAVA程序 003.输入项目的名字为mybatis001 004.我们对这个项目添加Support,各种框架依赖 ...
- CentOS7 防火墙设置
CentOS7 防火墙命令 最近在公司服务器上安装了oracle12c数据库,在用数据库客户端连接的时候,连接不了.最后查找资料的原因是因为oracle的服务端口未开放. 首先还是还是输入以往的开启某 ...
- Problem C Updating a Dictionary
Problem C Updating a Dictionary In this problem, a dictionary is collection of key-value pairs, ...
- JS - 对话框
1,<span onclick="return confirmAct();">执行操作</span> 2, function confirmAct(){ i ...
- Arduino 的读串口与写串口
//准备一下 while(Serial.available()>0) WifiSerial.write(Serial.read()); wh ...
- systemctl无法停掉keepalived
这个问题搞了好半天,记录一下,启停都是用的systemctl 起初是测试vip漂移时候发现,主备节点都开启keepalived的状况下,一切正常,主节点的vip也可以访问. 第一次停掉主节点的keep ...
- border-radius 在 浏览器开发者工具移动端里是有效的,在真机是无效的。
border-radius 在 浏览器开发者工具移动端里是有效的,在真机是无效的,怎么解决? 答案是 border-radius:20px !important 加上!important 就好了.
- Web安全常见问题及解决方法
关于Web安全,我们最早听到最多的就是SQL注入.例如用户在系统登录界面输入用户名和密码,提交以后,后端直接拿到数据就拼接SQL语句去查询数据库.如果在输入时进行了恶意的SQL拼装,那么最后生成的SQ ...
- UVA - 11181 Probability|Given (条件概率)
题意:有n个人,已知每个人买东西的概率,求在已知r个人买了东西的条件下每个人买东西的概率. 分析:二进制枚举个数为r的子集,按定义求即可. #include<cstdio> #includ ...
- POJ 2031:Building a Space Station 最小生成树
Building a Space Station Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 6083 Accepte ...