LuoguP5139 z小f的函数 题解

Content

给定 \(T\) 个二次函数 \(y=ax^2+bx+c\)，有若干次操作，有一个操作编号 \(p\)，保证仅为以下这五种：

• 操作 \(1\)：给定 \(k\)，将函数图像向上移动 \(k\) 格（\(k<0\) 就是向下移动 \(-k\) 格）。
• 操作 \(2\)：给定 \(k\)，将函数图像向右移动 \(k\) 格（\(k<0\) 就是向左移动 \(-k\) 格）。
• 操作 \(3\)：给定 \(k_1,k_2\)，将函数图像关于点 \((k_1,k_2)\) 对称。
• 操作 \(4\)：给定 \(k_1,k_2\)，求函数图像在闭区间 \([k_1,k_2]\) 内的最大值和最小值并输出（保留 \(2\) 位小数）。
• 操作 \(5\)：给定 \(u,v,w\)，求 \(y=ax^2+bx+c\) 的函数图像是否和 \(y=ux^2+vx+w\) 的函数图像有焦点，有的话输出 2，否则输出 0。

在所有操作弄完以后，你还需要给出操作完以后函数的最值（显然，根据 \(a\) 的正负来判定，保留 \(2\) 位小数）。

Range

1. 关于 \(T,m\)，有 \(T\leqslant 10,m\leqslant 10000\)。
2. 关于其他的变量，保证 \(a\neq0,u\neq0,a\neq u,1\leqslant p\leqslant5,-100\leqslant a,b,c,k_1,k_2,k,u,v,w\leqslant 100\)。

Solution

我使用的是一般式进行操作。这么做的优点是，你不需要花多余的时间来求顶点式 \(a(x-h)^2+k\) 中的 \(h\) 和 \(k\)，前期处理比较方便，但问题是后面的计算量非常大，没心理准备根本就是做到一半就崩溃了。所以，这篇题解旨在帮助大家多见识一些复杂的计算，让你从容应对这么多复杂的式子和分类讨论。

话不多说，开始处理每个操作：

Part 1 操作 \(1\)

很显然，我们将其上下移动以后改变的只是常数项的值。

什么什么，你还要我讲原因？

那就请看图吧：

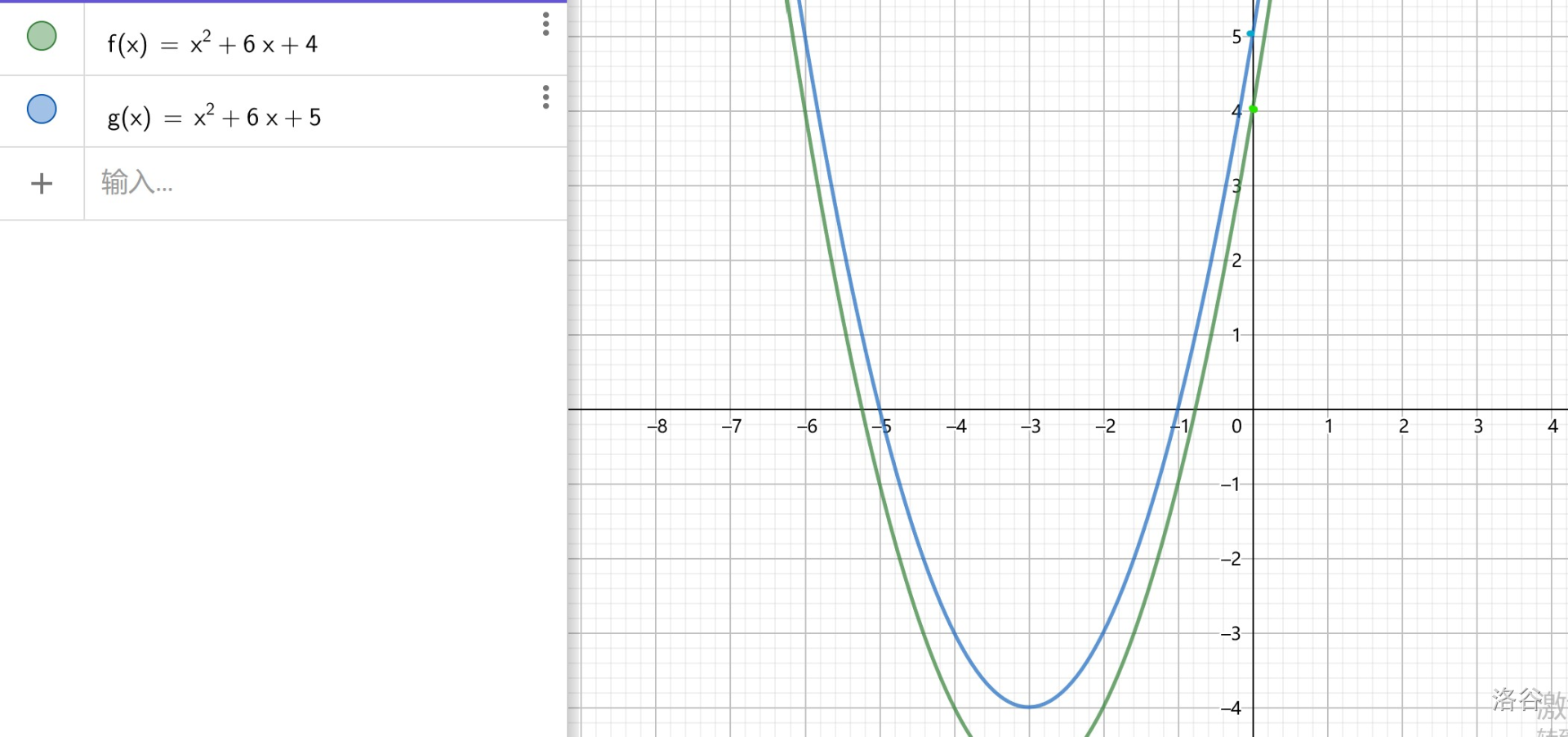
上图中蓝色的曲线是函数 \(y=x^2+6x+5\) 的图像，而绿色的曲线是函数 \(y=x^2+6x+4\) 的图像。我们可以看到，蓝色的曲线和 \(y\) 轴的交点是 \((5,0)\)，而绿色的曲线和 \(y\) 轴的交点为 \((4,0)\)，所以正好和常数项相对应。

或者我们也可以这样：

设 \(y_1=a_1x^2+b_1x+c_1,y_2=a_2x^2+b_2x+c_2\)。

令两个函数的 \(x\) 都等于 \(0\)，分别代入两个函数中可得 \(y_1=c_1,y_2=c_2\)。

本来这个很显然的，但我想为了照顾那些还没有学二次函数的学弟，所以还是写写吧。

故，操作后的函数为 \(y=ax^2+bx+c+k\)。

Part 2 操作 \(2\)

这个用顶点式的话很方便，但是我们这里只提一般式的做法，不过会借用一下顶点式。

首先，我们可以由顶点式 \(y=a(x-h)^2+s\)（由于为避免与题面中的 \(k\) 重复，故改为 \(s\)）向右平移 \(k\) 格后的式子为 \(y=a(x-h-k)^2+s\)，然后再把它拆开，得到：\(y=ax^2-(2ak+2ah)x+ah^2+ak^2+2ahk+s\)。又由于我们知道 \(h=-\dfrac{b}{2a},s=\dfrac{4ac-b^2}{4a}\)，所以，直接将它强算过来，可以得到 \(y=ax^2+(b-2ak)x+ak^2-bk+c\)。

故，操作后的函数为 \(y=ax^2+(b-2ak)x+ak^2-bk+c\)。

Part 3 操作 \(3\)

首先，我们令一个在抛物线上的点为 \((x_0,y_0)\)，所以我们就有在与 \((k_1,k_2)\) 对称后的坐标为 \((2k_1-x_0,2k_2-y_0)\)。

什么什么，要我讲原因？

可以，那请听我说：由于它们的横坐标和纵坐标之差分别为 \((x_0-k_1,y_0-k_2)\)，所以它的对称点的坐标为 \((k_1-(x_0-k_1),k_2-(y_0-k_2))\Rightarrow(2k_1-x_0,2k_2-y_0)\)。

那么我们再代入到 \(y=ax^2+bx+c\) 中可得：\(2k_2-y_0=a(2k_1-x_0)^2+b(2k_1-x_0)+c\)，因此可得到 \(y_0=2k_2-a(2k_1-x_0)^2-b(2k_1-x_0)-c\)。

那么再对右边的式子进行化简，然后再合并 \(x\) 同类项，可得到 \(y_0=-ax_0^2+(4ak_1+b)x_0+2k_2-4ak_1^2-2bk_1-c\)。

故，操作后的函数为 \(y=-ax^2+(4ak_1+b)x+2k_2-4ak_1^2-2bk_1-c\)。

Part 4 操作 \(4\)

这一段是我们的重头戏。

首先根据 \(a<0\) 和 \(a>0\) 两大类，再通过 \(k_1,k_2\) 以及 \(x'=-\dfrac{b}{2a}\) 之间的关系进行分类讨论。

笔者温馨提示：自己画一个函数图像具体分析，下面的两个图中作为例子的函数解析式左边有。

好的，那么现在就开始吧。

4.1 \(a<0\)

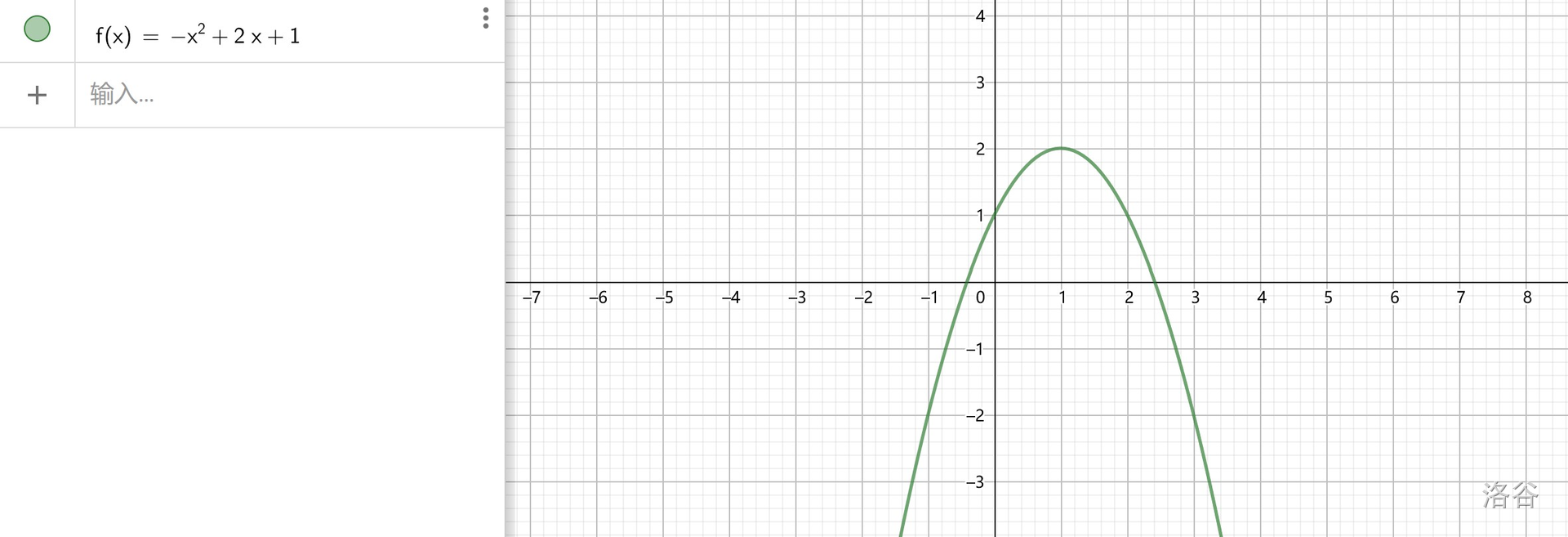
那么这时候还需要 \(4\) 种情况来分类讨论：

1. \(k_2<x'\)，此时可以从图像上看到，\(y_{\min}=ak_2^2+bk_2+c,y_{\max}=ak_1^2+bk_1+c\)。

2. \(k_2\geqslant x,k_1<x'\) 且 \(k_2-x'<x'-k_1\)，此时可以从图像上看到，\(y_{\min}=ax'^2+bx'+c,y_{\max}=ak_1^2+bk_1+c\)。

3. \(k_2\geqslant x,k_1<x'\) 且 \(k_2-x'\geqslant x'-k_1\)，此时可以从图像上看到 \(y_{\min}=ax'^2+bx'+c,y_{\max}=ak_2^2+bk_2+c\)。

4. \(k_1\geqslant x\)，此时可以从图像上看到 \(y_{\min }=ak_1^2+bk_1+c,y_{\max}=ak_2^2+bk_2+c\)。

4.2 \(a>0\)

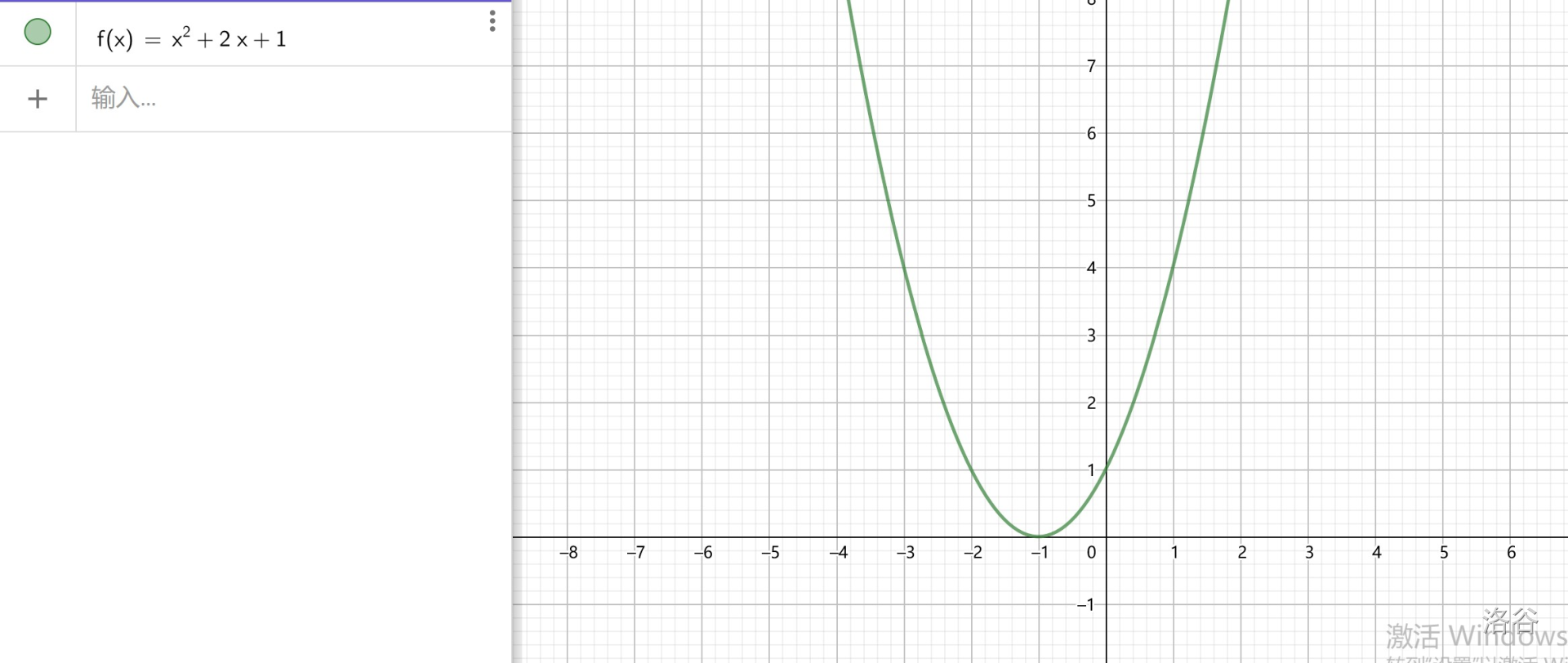
同样，这时候还需要 \(4\) 种情况来分类讨论：

1. \(k_2<x'\)，此时可以从图像上看出 \(y_{\min}=ak_1^2+bk_1+c,y_{\max}=ak^2+bk_2+c\)。

2. \(k_2\geqslant x,k_1<x'\) 且 \(k_2-x'<x'-k_1\)，此时可以从图像上看到 \(y_{\min}=ak_1^2+bk_1+c,y_{\max}=ax'^2+bx'+c\)。

3. \(k_2\geqslant x,k_1<x\) 且 \(k_2-x'\geqslant x'-k_1\)，此时可以从图像上看到 \(y_{\min}=ak_2^2+bk_2+c,y_{\max}=ax'^2+bx'+c\)。

4. \(k_1\geqslant x\)，此时可以从图像上看到 \(y_{\min}=ak_2^2+bk_2+c,y_{\max}=ak_1^2+bk_1+c\)。

至此，所有的分类讨论就完了，直接判断条件对应输出结果就好。

Part 5 操作 \(5\)

这个倒比操作 \(4\) 简单，直接联立一下就得到 \(ax^2+bx+c=ux^2+vx+w\)。所以，我们就只需要判断这个方程是否有实数根就好了。

我们将上面这个方程移项，可以得到 \((a-u)x^2+(b-v)x+c-w=0\)，所以，我们可以得到 \(\triangle=(b-v)^2-4(a-u)(c-w)\)。根据 \(\triangle\) 可以判别出这个方程实数根的情况，也就可以判断这两个函数图像是否有交点了。具体如下——

当 \(\triangle\geqslant 0\) 时，这个方程有实数根，这两个函数图像也就有交点了；否则，当 \(\triangle<0\) 时，这个方程没有实数根，这两个函数图像也就没有交点了。

至此，用一般式解决本题的算法也就讲完了。顶点式的话题解区里的大佬们已经讲得很清楚了。

如有不懂的话，下面的代码也许能帮助你。

Code

#include <cstdio>
#include <algorithm>
using namespace std;

int t;

double f(double a, double b, double c, double x) {
	return a * x * x + b * x + c;
}

int main() {
	scanf("%d", &t);
	while(t--) {
		double a, b, c;
		int m;
		scanf("%lf%lf%lf%d", &a, &b, &c, &m);
		while(m--) {
			int opt;
			scanf("%d", &opt);
			if(opt == 1) {
				double k;
				scanf("%lf", &k);
				double a0 = a, b0 = b, c0 = c + k;
				a = a0, b = b0, c = c0;
			}
			else if(opt == 2) {
				double k;
				scanf("%lf", &k);
				double a0 = a, b0 = b - 2 * a * k, c0 = a * k * k - b * k + c;
				a = a0, b = b0, c = c0;
			}
			else if(opt == 3) {
				double k1, k2;
				scanf("%lf%lf", &k1, &k2);
				double a0 = -a, b0 = 4 * a * k1 + b, c0 = 2 * k2 - 4 * a * k1 * k1- 2 * b * k1 - c;
				a = a0, b = b0, c = c0;
			}
			else if(opt == 4) {
				double k1, k2, xp = -(b / (2 * a)), yp = (4 * a * c - b * b) / (4 * a);
				scanf("%lf%lf", &k1, &k2);
				if(a > 0) {
					if(k2 < xp)	{
						printf("%.2lf %.2lf\n", f(a, b, c, k2), f(a, b, c, k1));
					}
					else if(k1 < xp) {
						if(k2 - xp < xp - k1) {
							printf("%.2lf %.2lf\n", f(a, b, c, xp), f(a, b, c, k1));
						}
						else if(k2 - xp >= xp - k1) {
							printf("%.2lf %.2lf\n", f(a, b, c, xp), f(a, b, c, k2));
						}
					} else {
						printf("%.2lf %.2lf\n", f(a, b, c, k1), f(a, b, c, k2));
					}
				} else if(a < 0) {
					if(k2 < xp)	{
						printf("%.2lf %.2lf\n", f(a, b, c, k1), f(a, b, c, k2));
					}
					else if(k1 < xp) {
						if(k2 - xp < xp - k1) {
							printf("%.2lf %.2lf\n", f(a, b, c, k1), f(a, b, c, xp));
						}
						else if(k2 - xp >= xp - k1)	{
							printf("%.2lf %.2lf\n", f(a, b, c, k2), f(a, b, c, xp));
						}
					} else {
						printf("%.2lf %.2lf\n", f(a, b, c, k2), f(a, b, c, k1));
					}
				}
			}
			else if(opt == 5) {
				double u, v, w;
				scanf("%lf%lf%lf", &u, &v, &w);
				double delta = (b - v) * (b - v) - 4 * (a - u) * (c - w);
				puts(delta < 0 ? "0" : "2");
			}
		}
		printf("%.2lf\n", (4 * a * c - b * b) / (4 * a));
	}
	return 0;
}