png crc讲解

　　我太难了。

　　我真的是为你们着想，你们学姐说misc太简单了，可就是这么简单我相信你们也不会做。。。我还得给你们讲解。。。

加油吧！！！

　　工具：010editor    这个我想给你放下载链接来着，后来仔细想想，不行。。。自己去装好这个软件。

　　在这里我用一道类似的题来给你们讲，首先会下载到一个png的图片。

　　　就像这种的，然后你用010editor打开这个图片你会看到这个图片的二进制数据。

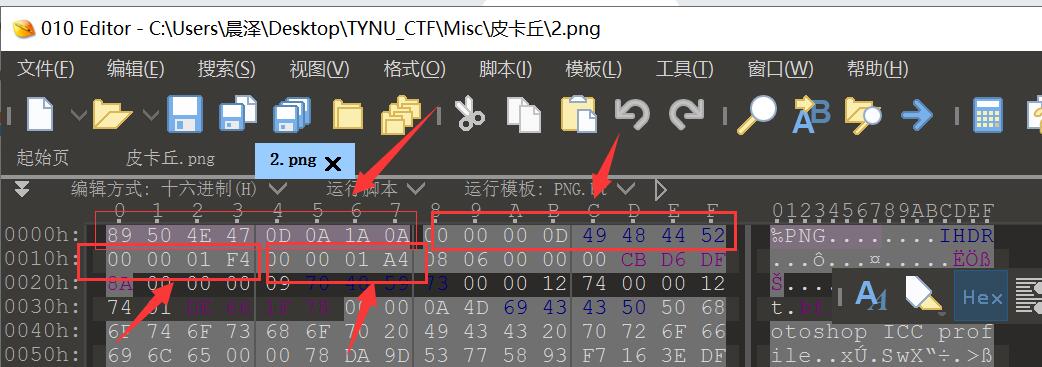
　　这里我简单讲一下圈住的数据代表什么，第一个箭头指向的，是文件的文件头，这个是固定的，所有的png格式的文件头都是89 50 4E 47 0D 0A 1A 0A 。

　　第二个箭头指向的，前四个字节00 00 00 0D（即为十进制的13）代表数据块的长度为13，数据块包含了png图片的宽高等信息，该段格式是固定的。之后的四个字节49 48 44 52（即为ASCII码的IHDR）是文件头数据块的标示，该段格式也是固定的。

　　重点来了！！！

　　第一个箭头，四个字节00 00 01 F4（即为十进制的500），代表该图片的宽，该段数据是由图片的实际宽决定的。

　　第二个箭头，四个字节00 00 01 A4（即为十进制的420），代表该图片的高，该段数据是由图片的实际高度决定的。

　　所以这道题你只需要，将图片的宽或者高稍微改大一点点，就可以看到隐藏的flag了。！！

　　思路说完了，至于你们怎么修改，怎么保存。就是你们的事了！已经很清楚了。。。

　　晒一下所讲的这道题修改完的图片。

　　

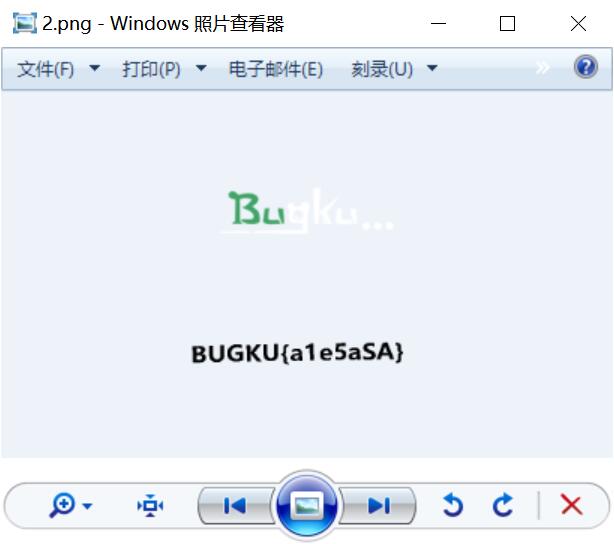
　　其实这种题是可以进行crc爆破能爆破出真实的高和宽的，但是这题还用不到，就不教你们了。希望你们可以有一天来学习crc爆破，到时候回头看这道题，你会觉得，真简单！