De Moivre–Laplace theorem 掷硬币

De Moivre–Laplace theorem - Wikipedia https://en.wikipedia.org/wiki/De_Moivre%E2%80%93Laplace_theorem

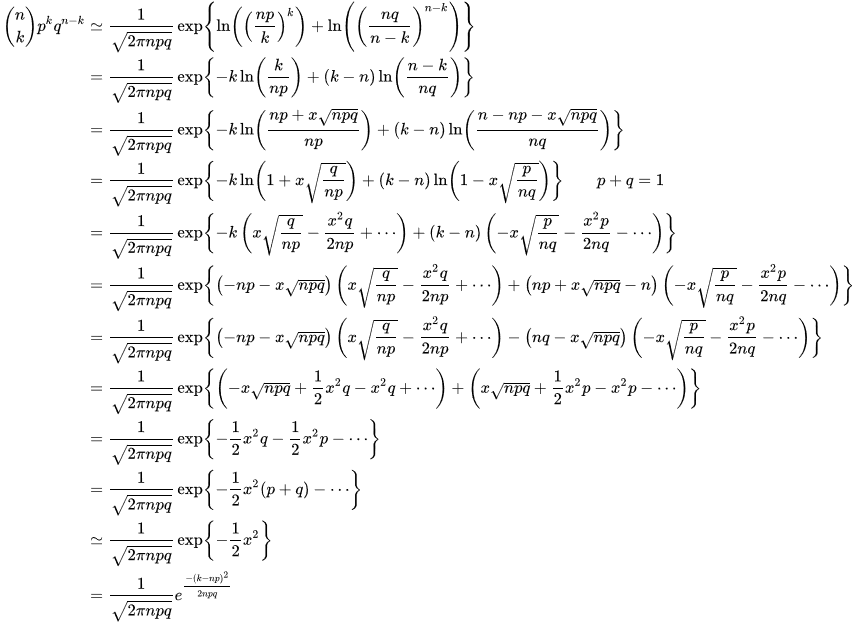
https://baike.baidu.com/item/棣莫弗—拉普拉斯定理/5784346

棣莫弗—拉普拉斯定

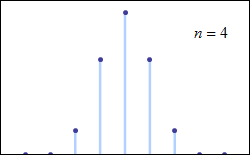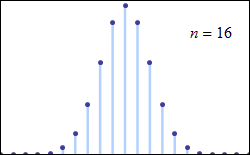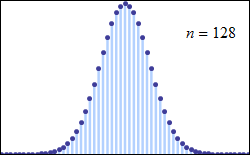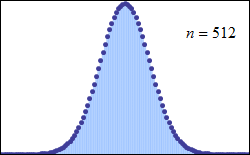
File:De moivre-laplace.gif - Wikipedia https://en.wikipedia.org/wiki/File:De_moivre-laplace.gif

De_moivre-laplace.gif ‎(250 × 155 pixels, file size: 21 KB, MIME type: image/gif, looped, 8 frames, 18 s)

 

 Consider tossing a set of n coins a very large number of times and counting the number of "heads" that result each time. The possible number of heads on each toss, k, runs from 0 to n along the horizontal axis, while the vertical axis represents the relative frequency of occurrence of the outcome k heads. The height of each dot is thus the probability of observing k heads when tossing n coins (a binomial distribution based on n trials). According to the de Moivre–Laplace theorem, as n grows large, the shape of the discrete distribution converges to the continuous Gaussian curve of the normal distribution.