AcWing 94. 递归实现排列型枚举

AcWing 94. 递归实现排列型枚举

题目链接

把 1~n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数n。

输出格式

按照从小到大的顺序输出所有方案，每行1个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围

1≤n≤9

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

题解

从小到大的顺序枚举，就会得到字典序最小的序列

如果变量为全局变量，那么变量初值默认为0；

如果变量为局部变量，那么变量初值为随机值。

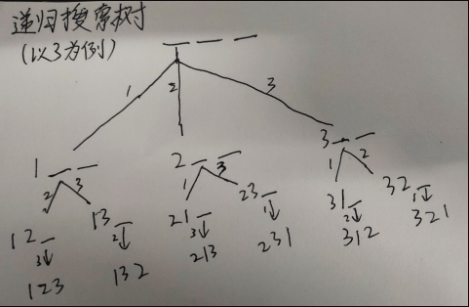
代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>

using namespace std;
const int N=10;//数据范围为1<=n<=9,我们是从i=1开始的，因此N取10；
int n;
int num[N];//0表示没有被遍历到，1~n表示放置了哪些数
bool st[N];//true  or  false(表示是否用过)
void dfs(int u)
{
	if(u>n)//表示已经枚举完毕
	{
		for(int i=1;i<=n;i++)	cout<<num[i];
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++)
	if (!st[i])//如果第i个数没有被用过
	{
		num[u]=i;
		st[i]=true;
		dfs(u+1);

		num[u]=0;//又回到最初的状态，结合我发的题解图片去理解
		st[i]=false;
	}
}
int main()
{
	cin>>n;
	dfs(1);
	return 0;
}