GDUFE-OJ 1070上班打卡 ^位运算

GOJ1070 

思路1：运用位运算符‘ ^ ’，运用A^B^B=A的原理，直接求解

 #include <stdio.h>
 int main()
 {
     int n,i,b,a;
     while(scanf("%d",&n)!=EOF&&n!=)
     {
         b=;
         for(i=;i<*n-;i++)
         {
             scanf("%d",&a);
             b=b^a;
         }
         printf("%d\n",b);
     }
     return ;
 }

思路2： 全部输入后，sort排序，检索出落单的数字。

 #include<stdio.h>
 #include<algorithm>
 using namespace std;
 int ch[]={};
 int main()
 {
     int a,n,i;
     while(scanf("%d",&n)!=EOF&&n!=)
     {
         a=;
         for(i=;i<*n-;i++)
             scanf("%d",&ch[i]);
           sort(ch,ch+(*n-));
             for(i=;i<*n-;i+=)
                 if(ch[i]!=ch[i+])
                 {
                 a=;
                 break;
                 }
             if(a==&&i==*(n-)) printf("%d\n",ch[*n-]);
             else printf("%d\n",ch[i]);
     }
     return ;
 }

思路3：因为公司人数最大50000，打卡编号也是50000，假设人数50000；假设一一对应，那么直接开ch[50000]={0}，然后将输入的打卡编号对应的数组下标的数组的值+1，最后检索，落单的编号的值是1，其余是2。可得答案。此方法好投机取巧，妙哉。

A^0=A,A^B^B=A 。位运算符还是很有用的。

GOJ1203

思路：快速幂求a^b，然后mod c。因为是随便输入的a，b，所以范围很大，而题目只需求最后三位，所以百位以上的计算不用理了，直接%1000。

 #include <stdio.h>
 int main()
 {
     unsigned long long a,b;
     while(scanf("%llu%llu",&a,&b)!=EOF)
     {
         unsigned long long c=,d=a;
         while(b!=)
         {
         if(b&!=)//如果是0则无需计算，因为n*1=n
             c*=d%;
             d*=d%;
             b>>=;
         }
         if(c%>)
         printf("%llu\n",c%);
         else if(c%>)
         printf("0%llu\n",c%);
         else
         printf("00%llu\n",c%);
     }
     return ;
 }

Tip：以上mod c是因为怕数字过大爆了，一是因为a的b次mod c，二是因为早晚要mod c，所以早mod 无所谓。

小知识：

快速幂原理：a^b,将b拆成二进制数相加的形式，从而使运算次数减少

Example：a^11=a^(2^0+2^1+2^3)，时间复杂度为O（log11）。

 scanf("%d%d",&a,&b)
         int c=,d=a;
         while(b!=)
         {
         if(b&!=)//取b的二进制数的最后一位（相当于b%2!=0）
             c*=d;
             d*=d;  //每往右推一位，d倍增，2^0 2^1 2^2……
             b>>=;//将b的二进制数往右推一位（相当于b/=2）
         }
 printf("%d\n",c);//c=a^b

GOJ1359

 思路：先将1-500000的所有素数筛出，并在此过程中筛出含‘33’的数，最后在L到R之间计数。

 #include <stdio.h>
 #include <string.h>
 int ch[],ch33[],k=;

 int is33(int l)//筛出包含‘33’的数
 {
     while(l>)
     {
         if(l%==)return ;
         l/=;
     }
     return ;
 }

 void judge()//判断素数（埃氏筛法）
 {
     long long  i,j;
 memset(ch,-,sizeof(ch));//将ch所有元素初始化为-1
     for(i=;i<=;i++)
         if(ch[i]==-)
         {
             if(is33(i))
                 {
                     ch33[k++]=i;//存入ch33数组
                 }
         for( j=i*i;j<=;j+=i)
             ch[j]=;
         }
 }

 int main()
 {
     int n,s=,g,a,L,R,i;
     judge();
     while(scanf("%d",&n)!=EOF)
     while(n--)
     {
         s++;
         scanf("%d%d",&L,&R);
         for(g=,a=;g<k;g++)
         {
                 if(ch33[g]>=L&&ch33[g]<=R)a++;
                 if(ch33[g]>R)break;
         }
         printf("Case #%d: %d\n",s,a);
     }
     return ;
 }

以下是埃氏筛法的示意图：

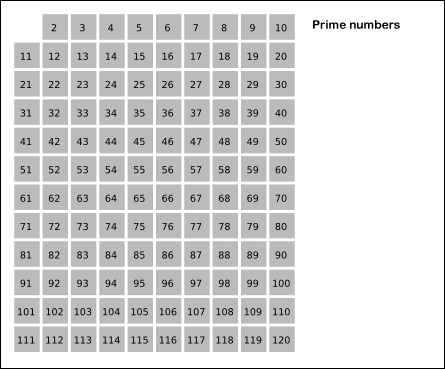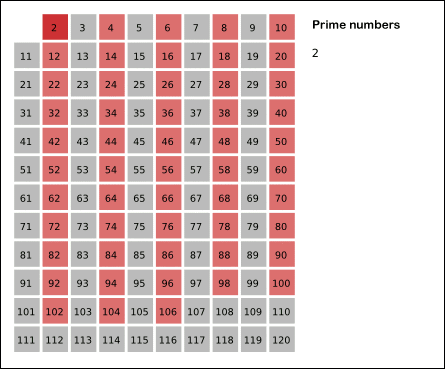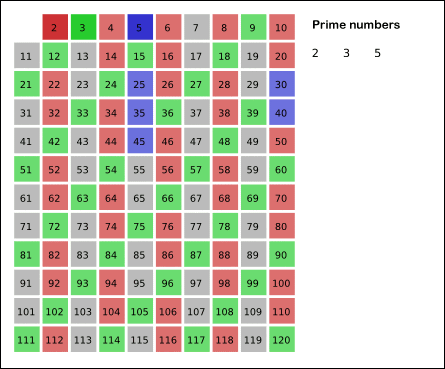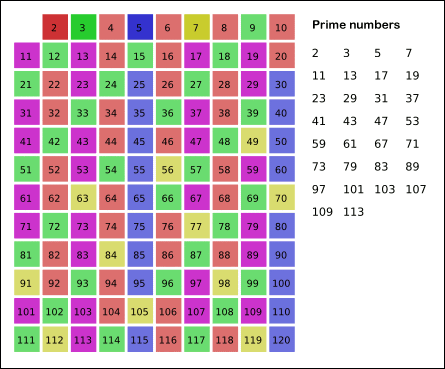
原理：

1.  根据算术基本定理（百度）：任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积。

2.  先用2筛，筛走不是素数的数（也就是2的倍数），接着用3,5,7……直到最后一位。

3.  被筛走的可以标记，后面就不再用这个数筛。

Tips：

1.sizeof是判断数据类型或者表达式长度符，用于计算有多少个字节。

sizeof(int)==4。

char ch[10]="abc",sizeof(ch)==10*1。

2.strlen是求字符串（仅字符串）长度的函数。char ch[10]="abc",strlen(ch)==3.

3.memset

void *memset(void *s, int ch, sizeof(n));

解释：将s中当前位置后面的n个字节 (typedef unsigned int size_t)用 ch 替换并返回 s 。

对数组操作时只能用于数组的置0或-1，其他值无效。

memset(ch,-1,sizeof(ch))就是将数组ch中所有元素替换为-1，返回ch。