[stat.simulation] Hasting-Metropolis Algorithm

• 问题背景：我们有一些观测数据X，这些数据假设是取值为1,...,m；我们还知道每个数据观测到的频数为:

　　但是我们现在无法计算B的大小。（这是一个假设，毕竟计算一串数字的和不是难事）

• 问题： 我们需要通过仿真产生一串随机变量，并且它们的概率分布函数为：

• 分析：如果B是可以计算的，那么(j)自然也是可以计算的。然后自然很容易随机生成服从这个概率分布的一串随机数。但是B不能计算。。。我们可以采用一个曲线救国的方案。

　　直观上来考虑这个问题，产生随机数时是一个一个地产生随机数，每个随机数取值为1,...,m中某一个。我们可以：

1）把一个随机数看成一个状态；

2）一个随机数的产生取决于前一个随机数，那么每个状态取决于前一个状态；

• 问题等效：对于状态{1,...,m}，有某个Markov Chain状态转移矩阵P，,随机选择一个初始状态，根据状态转移矩阵P,，依次产生一个状态序列。但是，重点是我们需要设计这个转移矩阵P，使得最终的产生的状态序列的概率分布为，也就是说这个Markov Chain的最终稳定状态时各个状态的概率分布为。

• Hasting-Metropolis算法描述

　　算法引入了一个随机选择的Markov Chain转移矩阵Q，。注意Q不是上面讲的P，而是用来构造P的一个辅助状态转移矩阵。构造的过程：

1） 根据Q，从当前状态，设为i，转移到状态下一个状态，设为j；

2）引入另一个概率函数，这个概率决定转移到下一个状态j或者停留在现在的状态i；

结合上述1,2）可以得到一个新的转移矩阵，并且可以经过精心构造，使得这个矩阵作为解决“等效问题”中的P矩阵，下面来看如何“精心构造”：

根据1,2）

根据平稳Markov Chain的“时序可逆”性质：

or

因为是一个概率值，必须小于1，所以最终的构造为：

但是是未知的（因为B无法求值），好在上式中是(i)/(j)=b(i)/b(j)，那么：

• Hasting-Metropolis算法流程

1） 选择一个不可约Markov Chain概率转移矩阵；随机选择初始状态;

2)  let n=1, X[n]=k;

3) 生成随机数，生成随机数 U∈（0, 1）

4) 如果，则选择NS=X；否则选择NS=X[n];

5) n=n+1, X[n]=NS;

6) go to 3)

说明，以上在讨论函数和算法流程中，都没有特别考虑i = j的情况。原因是i=j时“不失一般性”。此时=1，算法步骤4）一定会选择NS=X,而此时X==X[n]。所以，算法步骤3）中如果产生的X==X[n]，那么4）定然会保持原来状态从而X[n+1]<-X[n]。

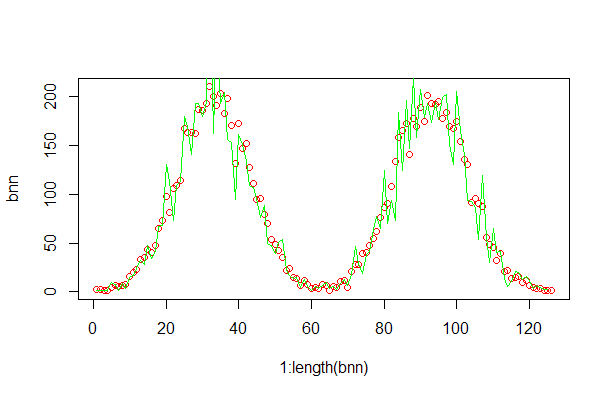
• 仿真例子

通过R语言实现用H-M算法采样服从混合高斯分布密度函数。

主程序：

source("intgMatrix.R")
source("sampleByPr.R")

FF = 10000# sample points

br<-rnorm(FF/2, 0, 10)
br2<-rnorm( FF/2, 60, 10)
br <- c(br, br2)
br<-round(br)

tbl <- table(br)

b<-unname(tbl)   # a sequence of number

m <- length(b)
#generate Q
r<-c()
for(i in 1:m)
{
  r_ <- runif(m, 0, 1)
  r_ <- r_ / sum(r_)  # nomalize
  r<- c(r, r_)
}
Q<- t(matrix(r, m, m))
Qint <- intgMatrix(Q)     # row-based integral

# start to sample sn data
sn = FF  # #sample
X <- c()  # sample data (index of b)

# initial step
k<- round(runif(1, 1, m))
X[1] <- k

# interation steps
for(n in 1:(sn-1))
{
  PrX_j <- Qint[X[n], ]  # last sample's index as row-index in Q
  while(TRUE){
    X_tmp <- X[n]
    X_tmp <- sampleByPr(PrX_j) # the index of X[n]
    if(X_tmp != X[n]){
      break
    }
  }

  U <- runif(1, 0, 1)
  # for alph(i, j)
  al_ <- (b[X_tmp] * Q[X_tmp, X[n]]) / (b[X[n]] * Q[X[n], X_tmp])
  if(al_ > 1){al_ <- 1}
  NS <- X[n]
  if(U < al_) {
    NS <- X_tmp
  }

  X[n + 1] <- NS

}

# plot

bnn<-as.numeric(b)
plot(1:length(bnn),bnn,col="red")
Xnn <- as.numeric(table(X))
lines(1:length(Xnn),Xnn/rt,col="green")

概率积分矩阵，Qi[i,k]=∑_j=1,..,kQ[i,j]

intgMatrix <- function(Q)
{
  Qi<-matrix(nrow=dim(Q)[1], ncol = dim(Q)[2])
  Qi[, 1] = Q[,1]
  for(i in 1:dim(Q)[1]){
    for(j in 2:dim(Q)[2]){
      Qi[i,j] <- Qi[i, j- 1] + Q[i, j]
    }
  }
  return(Qi)
}

根据概率积分向量生成采样点。

概率积分向量pi[i]=∑_j=1,..,ip[i],其中p[i]=Pr{X=i}为原始概率分布

sampleByPr <- function(Pr_vector)
{
  ru <- runif(1,0,1)

  for(i in 1:length(Pr_vector)){
    if(Pr_vector[i] > ru){
      return(i)
    }
  }
}