经典矩阵快速幂之一-----poj3233(矩阵套矩阵

　　题意：给你一个矩阵A，求S=A+A^2+A^3+...+A^k。

　　其实这个当时我看着毫无头绪，看了他们给的矩阵发现好！精！妙！

　　我们这样看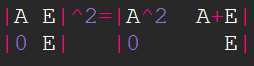

　　　　　　　

　　　　　　　　　

　　　是不是有点思路！

　　 没错！就是右上角，我们以此类推可以得到A+A^2+A^3+...+A^k+E，我们只要再减去个单位矩阵就好了。

　　 但是！我矩阵里面怎么套矩阵！肿！么！办！其实很简单，一个n*n的矩阵,我们可以把它看成(2*n)*(2*n)的矩阵，就把他分成了四份，就如上图所示，就很简单了！

　　注意下小坑点：减了可能就负了，后面减完要加个mod(ง •_•)ง

#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<cstring>
#include<queue>
#include<set>
#include<string>
#include<map>
#include <time.h>
#define PI acos(-1)
using namespace std;
typedef long long ll;
typedef double db;
const int maxn = ;
const int N = ;
const ll maxm = 1e7;
const int INF = 0x3f3f3f;
const ll inf = 1e15 + ;
const db eps = 1e-;
ll n, k, mod;
struct Matrix{
    ll mat[maxn][maxn];
    Matrix operator*(const Matrix& m)const{
        Matrix tmp;
        for (int i = ; i <= n; i++) {
            for (int j = ; j <= n; j++) {
                tmp.mat[i][j]=;
                for (int k = ; k <= n; k++) {
                    tmp.mat[i][j] += mat[i][k]*m.mat[k][j]%mod;
                    tmp.mat[i][j]+=mod;
                    tmp.mat[i][j] %= mod;
                }
            }
        }
        return tmp;
    }
};

int Pow(Matrix &m, int k) {
    Matrix ans;
    memset(ans.mat ,  , sizeof(ans.mat));
    for (int i=; i<=n; i++) {
        ans.mat[i][i]=;
        ans.mat[i+n][i+n]=;
    }
    n*=;
    while(k){
        if(k&)
           ans = ans*m;
        k >>= ;
        m = m*m;
    }
    n/=;
    for (int i=; i<=n; i++) {
        ans.mat[i][i+n]--;
        ans.mat[i][i+n]+=mod;
        ans.mat[i][i+n]%=mod;
    }
    for (int i=; i<=n; i++) {
        for (int j=; j<=n; j++) {
            if (j==n) printf("%d\n", ans.mat[i][j+n]);
            else  printf("%d ", ans.mat[i][j+n]);
        }
    }
}

void solve() {
    Matrix m;  memset(m.mat, , sizeof(m.mat));
    scanf("%lld%lld%lld", &n, &k, &mod);
    for (int i = ; i <= n; i++) {
        for (int j = ; j <= n; j++) {
            scanf("%lld", &m.mat[i][j]);
            m.mat[i][i+n]=;
            m.mat[i+n][i+n]=;
        }
    }
    k++;
    Pow(m, k);

}
int main() {
    int t = ;
    //freopen("in.txt", "r", stdin);
   // scanf("%d", &t);
    while(t--)
        solve();
    return ;
}